Maximum Likelihood Estimation
Binomial Model
We will use a simple hypothetical example of the binomial distribution to introduce concepts of the maximum likelihood test.
We have a bag with a large number of balls of equal size and weight. Some are white, the others are black. We want to try to estimate the proportion, &theta., of white balls. The chance of selecting a white ball is &theta.. Suppose we select ~n times replacing and mixing after each selection ("~{sampling with replacement}"). Then chance of selecting white ball is &theta. each time, and the individual trials (selections) are independent of each other.
The number, ~x, of white balls from the ~n trials is binomially distributed, that is:
p ( ~x | &theta. ) _ = _ ( ^~n _~x ) (&theta.)^{~x} (1 - &theta.)^{~n - ~x} _ _ _ &theta. &in. [ 0 , 1 ]
where _ ( ^~n _~x ) _ = _ ~n#! ./ ~x#! ( ~n - ~x )#! _ = _ ~n (~n - 1) ... (~n - ~x + 1) ./ ~x#! _ _ _ [ ~x terms top and bottom]
You will probably recognize this as the binomial distribution with parameters ~n and &theta..
Maximum Likelihood Estimator
Suppose now that we have conducted our trials, then we know the value of ~x (and ~n of course) but not &theta.. This is the reverse of the situation we know from probability theory where we assume we know the value of &theta. from which we can work out the probability of the result ~x, i.e. the probability of ~x given &theta., ~p ( ~x | &theta. ).
What is the ~{likekihood} of the parameter having a value &theta. when the result of the experiment is ~x? (We use the word ~{likelihood} instead of ~{probability} to avoid confusion.) Define the #~{likelihood function}:
L( &theta. ) _ #:= _ L( &theta. | ~x ) _ #:= _ p( ~x | &theta. ) _ = _ ( ^~n _~x ) (&theta.)^{~x} (1 - &theta.)^{~n - ~x}
The greater L(&theta.) is the more "likely" that &theta. is the true value. To find the value of &theta. that maximizes L(&theta.), take logs and differentiate:
l(&theta.) _ = _ ln(L(&theta.)) _ = _ ln ( ^~n _~x ) + ~x ln(&theta.) + (~n - ~x) ln(1 - &theta.)
fract{&partial. l(&theta.),&partial.&theta.} _ = _ fract{~x ,&theta.} - fract{(~n - ~x),1 - &theta.}
fract{&partial. l(&theta.),&partial.&theta.} _ array{ > _ 0, _ _ _ _ _ _ &theta. _ < _ {~x/~n}/ = _ 0, _ _ _ _ _ _ &theta. _ = _ {~x/~n}/ < _ 0, _ _ _ _ _ _ &theta. _ > _ {~x/~n}}
So est{&theta.} = ~x/~n, is the value of &theta. for which L(&theta.) is greatest. This is called the #~{Maximum likelihood estimator} (MLE) of &theta..
Likelihood Ratio Test
Suppose that, instead of trying to estimate &theta., we have an a-priori idea about the value of &theta., i.e. we put the hypothesis H: &theta. = &theta._0, and we want to test to see if this is acceptable. Suppose we have conducted the trial and the number of white balls was ~x. Define the #~{likelihood ratio} as
LR( ~x ) _ = _ fract{L( &theta._0 | ~x ),L( est{&theta.} | ~x )}
Where est{&theta.} is the maximum likelihood estimate as defined above. So LR is the ratio of the likelihood for the hypothesis to the maximum likelihood. As est{&theta.} maximizes L( &theta. ) for any &theta. &in. [ 0 , 1 ], and &theta._0 is just one of these values, then _ 0 < LR =< 1 . _ (Obviously LR = 1 when &theta._0 = est{&theta.}, but remember that we don't know the value of est{&theta.} until we have conducted the trial.)
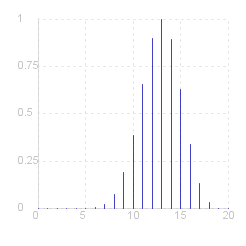 In the case of the binomial example we have been looking at:
In the case of the binomial example we have been looking at:
LR( ~x ) _ = _ fract{( &theta._0 )^{~x} ( 1 - &theta._0 )^{~n - ~x} ,( ~x/~n )^{~x} ( ( ~n - ~x )/~n )^{~n - ~x}}
_ _ _ _ _ = _ script{rndb{fract{~n &theta._0,~x}},,,~x,} script{rndb{fract{~n ( 1 - &theta._0 ),~n - ~x}},,,~n - ~x,}
Clearly this has maximum, LR = 1, when _ ~x = ~n &theta._0 , _ and falls off to either side of this value.
The diagram on the right plots the values of LR for ~n = 20 and H_0 : &theta. = 0.65 . Note that this has a maximum (of 1) at ~x = 20 # 0.65 = 13.
Significance Probability
Note that the likelihood ratio LR(~x) will be between 0 and 1, and the greater its value, the more acceptable the hypothesis is. But what criteria do we use to decide whether or not we accept the hypothesis? We define the #~{significance probability} (SP) of ~x as:
SP ( ~x ) _ = _ P\{ ~y | LR(~y) &leq. LR(~x) \}
I.e. this is the probability, given the hypothesis, of obtaining a result that is as likely or less likely than the obtained result.
It is possible, but messy to work this out explicitly (see Calculating MLE Statistics ), but modern computer packages make this a more realistic option. However it is still quite common to use approximations for SP, as is demonstrated on the Chi-squared Test for Binomial page.
In whichever way the SP is calculated, its main use is in deciding whether we accept the hypothesis or not. The usual procedure is to decide on an arbitrary #~{level} of the test, usually designated &alpha., where &alpha. = 5%, 1%, 0.5% etc. and reject the hypothesis if the SP is below this level.
#{Example}
Consider doing 20 samples with replacement in our white & black balls example, where we want to test the hypothesis that 65% of the balls are white (&theta. = 0.65). What is the significance probability of getting a result 11 white balls?
By looking at the graph of LR in the above section we can see that _ LR ( ~x ) =< LR ( 11 ) _ for _ 0 =< ~x =< 11 _ and _ 15 =< ~x =< 20.
P \{ 0 =< ~x =< 11 _ or _ 15 =< ~x =< 20 \} _ = _ B( 11 ; 20, 0.65) + 1 - B( 14 ; 20, 0.65) _ = _ 0.2376 + 1 - 0.7546 _ = _ 0.4830
( These values were calculated using the Mathyma binomial distribution look-up facility )
Confidence Interval
In the first section we showed that the MLE est{&theta.} = ~x/~n. This is a point estimate for &theta.. Although this is the most "likely" value for &theta. given the result it is unlikely that this is the exact true value of &theta..
We define the ~k% #~{confidence interval} as the range of values of &theta._0 for which SP > (100 - ~k)% - i.e. the range of values of &theta._0 for which we would accept the hypothesis H: &theta. = &theta._0, at the (100 - ~k)% level.
[ E.g. the usual value to use for the level of the test, &alpha., is 0.05 or 5%. The corresponding confidence interval is then (100 - 5)% or 95% ]
#{Example}
Continuing with our example, suppose we select a ball from the bag 20 times, and it turns out that the result is a white ball 7 times. From this we would conclude that the maximum likelihood estimator of &theta., the proportion of white balls in the bag, is 7/20 or est{&theta.} = 0.35. What is the 95% confidence interval?
If we had been testing the hypothesis H: &theta. = 0.35, then the significance probability of 7 white balls out of 20 would have been 100%.
For the hypothesis H: &theta. = 0.5, the S.P. would be 26.32% and we would accept the hypothesis. At &theta. = 0.6 the SP is 3.7% which would lead to rejection.
To three decimal places, the 5% S.P. is at &theta. = 0.580. (In fact the S.P. for &theta. = 0.580 is 6.73% => accept, while the S.P. for &theta. = 0.581 is 4.21% => reject.)
On the lower side S.P. = 1.27% for p = 0.135, S.P. = 6.69% for p = 0.136, so the confidence interval is 0.136 =< &theta. =< 0.580. Note that the point estimate of est{&theta.} = 0.35 is not exactly in the middle of the interval.
This method of trial and error is a somewhat laborious method of determining the confidence interval. A more practical way of calculating the confidence interval will be introduced after we have seen how to approximate a binomial distribution by a normal one.
Source for the graphs shown on this page can be viewed by going to the diagram capture page .