Discrete Random Variables

Discrete Random Variables

Consider the random variable _ ~X: &Omega. --> T , _ where the range space, T, is countable. Then _ ~X: ( &Omega., @A ) --> ( T, 2^T ) _ is called a #~{discrete random variable}.

Let T = \{~{t_i}\}_{~i &in. &naturals.}. The distribution of ~X is characterised by the numbers ( ~{p_i} )_{~i &in. &naturals.}, where

_ ~{p_i} _ = _ P( ~X = ~{t_i} ) _ = _ P ( \{ &omega. | ~X( &omega. ) = ~{t_i} \} )

[Note that the collection of sets _ ( \{ &omega. | ~X( &omega. ) = ~{t_i} \} )_{~{t_i} &in. T} _ forms a ( countable ) partition of &Omega.]

Clearly, if S &subset. T, then

P( ~X &in. S ) _ = _ P^~X( S ) _ = _ sum{ _ ~{p_i}, \{ ~i | ~{t_i} &in. S \},}

The numbers ( ~{p_i} )_{~i &in. &naturals.} are often referred to as "~{the distribution}" of the random variable. We are often only interested in these, and not so much in the underlying probability space ( &Omega., @A, P ) or the function ~X.

Integer-valued Random Variables

In the vast majority of cases of actual distributions we have _ T _ &subseteq. _ Z^+ , _ ( = \{ 0, 1, 2, ... \} ) .

Suppose we have a random variable _ ~X: ( &Omega., @A ) --> ( z^+ , 2^{z^+} ). The distribution of ~X is characterised by the numbers \{ ~p_~x \} _{~x = 0, 1, 2, ... } _ where

_ ~p_~x _ = _ P( ~X = ~x ) _ = _ P ( \{ &omega. | ~X( &omega. ) = ~x \} ,)

since the law of ~X, _ P ^~X ( A ) _ = _ P( ~X &in. A ) _ = _ &sum._{~x &in. A} _ ~p_~x. _ Note that ~p_~x >= 0 _ and _ &sum._{~x &in. Z^+} _ ~p_~x = 1. _

Conversely, if there is a sequence of real numbers _ ( &pi._{~x} )_{~x &in. Z^+} _ such that &pi._~x >= 0 _ and _ &sum._{~x &in. Z^+} _ &pi._~x = 1 , _ then we can construct a probability measure Q on ( &Omega., @A ):

Q( B ) _ = _ &sum._{~x &in. ~X( B )} _ &pi._~x , _ _ _ _ B &in. @A

From now on, by ~{discrete random variable} we mean a non-negative integer valued random variable.

Example

It is difficult to envisage a function from an abstract space. Here is a very simple example. The "experiment" involves the throw of two dice, one red say, and one blue. So the probability space &Omega. consists of 36 events represented here:

We suppose that the dice are fair, in which case the probability of each event is 1/36. Note that &Omega. is not a subset of &naturals.^2, but the set of the elements shown above, i.e. a pair consisting of a red die with a certain pattern of dots, and a blue die with a pattern of dots.

We now define a random variable, ~X, which maps each pair of dice in &Omega. to the sum of the number of dots on each die. So for example:

_	#{ --> 10}

But 10 also corresponds to the pairs _ and _ , so _ P( ~X = 10 ) _ = _ 3/36 _ = _ 1/12 . _ In fact ~X takes values from 2 to 12, so we can define the following :

~p_2 = 1/36 , _ ~p_3 = 2/36 , _ ~p_4 = 3/36 , _ ~p_5 = 4/36 , _ ~p_6 = 5/36 , _ ~p_7 = 6/36 , _ ~p_8 = 5/36 , _ ~p_9 = 4/36 , _ ~p_{10} = 3/36 , _ ~p_{11} = 2/36 , _ ~p_{12} = 1/36

Distribution Function

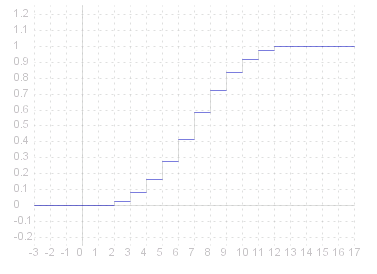
The #~{cumulative distribution function (c.d.f.)} of a discrete random variable is a step function, increasing at each value _ ~x , _ for which _ P( ~X = ~x ) > 0 .

Recall _ F_~X ( ~c ) _ = _ P( ~X =< ~c ) , _ so in the above example, P( ~X =< 2.5 ) = P( ~X =< 2 ) , thus F_~X is right continuous. Here is the graph of the distribution function for the dice example:

Expectation

If ~X is a discrete random variable with values _ \{~{x_i}\}_{~i &in. &naturals.} , _ with _ ~{p_i} _ = _ P( ~X = ~{x_i} ) , _ then the #~{expectation} of ~X is defined as

E( ~X ) _ = _ &sum._{~i &in. &naturals.} ~x_~i P( ~X = ~x_~i ) _ = _ &sum._{~i &in. &naturals.} ~x_~i ~p_~i

providing the series is absolutely convergent.

Note that the sum and therefore E( ~X ) may be infinite . _ ~X is said to have #~{finite expectation} if _ E( ~X ) < &infty. .

In the dice example,
_ _ _ _ E( ~X ) _ = _ 2 # 1/36 _ + _ 3 # 2/36 _ + _ ... _ + _ 12 # 1/36

by pairing the scores with the same probability we can write this
_ _ _ _ E( ~X ) _ = _ ( 2 + 12 ) # 1/36 _ + _ ( 3 + 11 ) # 2/36 _ + _ ... _ + _ ( 6 + 8 ) # 5/36 _ + _ 7 # 6/36
_ _ _ _ _ _ _ _ _ _ = _ 14 # ( 1/36 + 2/36 + 3/36 + 4/36 + 5/36 ) _ + _ 7 # 6/36
_ _ _ _ _ _ _ _ _ _ = _ (14 # 15 _ + _ 7 # 6 ) ./ 36 _ _ = _ _ 7 # 36 ./ 36 _ _ = _ _ 7

Note that in this case the expected value co-incides with the score with maximum probability. ~{This is not necessarily the case in all examples.}

Expectation as a Linear Operator

If ~X and Y are both real-valued discrete random variables then &alpha.~X + &beta.Y, where &alpha., &beta. &in. &reals., is also a real-valued discrete random variable.

Furthermore if ~X and Y both have finite expectation then so does &alpha.~X + &beta.Y, and

E( &alpha.~X + &beta.Y ) _ = _ &alpha.E( ~X ) + &beta.E( Y )

Indicator Function

A &in. @A. _ The indicator function _ 1_A : &Omega. --> \{0,1\} _ is a real-valued discrete random variable

E( 1_A ) _ = _ 1 &mult. P( &omega. &in. A ) + 0 &mult. P( &omega. &nin. A ) _ = _ P( A )

Markov's Inequality

Theorem:

If ~X is a real-valued discrete random variable and h: &reals. -> [0, &infty. ) is a function, and ~a >= 0, then

_

P ( &omega. | h( ~X( &omega. ) ) >= ~a ) _ _ =< _ _ fract{E( h( ~X ) ),~a}

Proof:

Put Y = h( ~X ) _ and _ A = Y^{-1}( [ ~a, &infty. ) ) = \{ &omega. | h( ~X( &omega. ) ) >= ~a \}. _ Now

• &omega. &in. A _ => _ h( ~X( &omega. ) ) >= ~a, _ ~a1_A ( &omega. ) = ~a
• &omega. &nin. A _ => _ h( ~X( &omega. ) ) >= 0, _ ~a1_A ( &omega. ) = 0

so h( ~X ) >= ~a1_A, _ and _ E( h( ~X ) ) >= E( ~a1_A ) = ~aE( 1_A ) = ~aP( A ) = ~aP( \{ &omega. | h( ~X( &omega. ) ) >= ~a \} )

Corollary: Markov's Inequality
If ~X is a real-valued discrete random variable, and ~a >= 0, then
_

P ( | ~X | >= ~a ) _ _ =< _ _ fract{E( | ~X | ),~a}

Variance

If ~X is a random variable and ~X ^2 has finite expectation, then we define the #~{variance}:

var( ~X ) _ = _ &sigma.^2 _ = _ &sigma._~X ^2 _ = _ E( [ ~X - E( ~X ) ]^2 )

Putting E( ~X ) = &mu. we have

&sigma.^2 _ = _ E( [ ~X - &mu. ]^2 ) _ = _ E( ~X ^2 - 2 &mu. ~X + &mu.^2 )

_ _ _ _ = _ E( ~X ^2 ) - 2 &mu. E( ~X ) + &mu.^2 _ = _ E( ~X ^2 ) - &mu.^2 _ = _ E( ~X ^2 ) - E( ~X )^2

Chebyshev's Inequality

Both the following inequalities are known as Chebyshev's Inequality _ ( ~a >= 0 in both cases ):

i ) _ _ _ _ _ _ _ _ P ( | ~X | >= ~a ) _ _ _ _ =< _ _ _ _ fract{E( ~X ^2 ),~a^2}

ii ) _ _ _ _ _ _ _ _ _ _ _ _ P ( | ~X - E( ~X ) | >= ~a ) _ _ _ _ =< _ _ _ _ fract{&sigma._~X ^2,~a^2}

Proof
i ) P ( | ~X | >= ~a ) _ = _ P ( ~X ^2 >= ~a^2 ) _ &le. _ E( ~X ^2 ) ./ ~a^2 _ ( by Theorem above ).
ii ) P ( | ~X - E( ~X ) | >= ~a ) _ = _ P ( ( ~X - E( ~X ) )^2 >= ~a^2 ) _ &le. _ E( ( ~X - E( ~X ) )^2 ) ./ ~a^2 _ = _ &sigma._~X ^2 ./ ~a^2

---