Mechanics

Velocity and Acceleration

Consider the universe as a system of interacting particles, moving relative to an agreed frame of reference. We are able to measure position and time. The position of a particle is given by a position vector ~#r, where #~r is time dependant, i.e. _ #~r _ = _ #~r (~t) , in other words the particle can move!

It is useful to define the two quantities #~{velocity}

~#v _ #:= _ deriv{~r} _ = _ fract{d#~r,d~t}

and #~{acceleration}

~#a _ #:= _ deriv2{#~r} _ = _ fract{d^2 #~r,d~t ^2} _ = _ fract{d#~v,d~t}

Mass

We attribute to each particle a quantity called #~{mass}. This has the property that if two particles are interacting - i.e. either attracting or repelling each other - then the particles will accelerate in the direction along the line joining them, and in opposite directions - i.e. they either accelerate towards each other or away from each other, and the magnitude of the accelerations is inversely proportional to their mass.

So if the particles have mass ~m_~i and position #~r_~i , ( ~i = 1, 2 ), their mass ratio is

_ _ _ ~m_1 #: ~m_2 _ = _ | deriv2{#~r_2} | #: | deriv2{#~r_1} |

and this is independent of the nature of the interaction, and does not change over time, or with position.

Given any third particle with mass ~m_3 and position #~r_3 , then

~m_1 #: ~m_2 _ = _ fract{~m_1 #: ~m_3,~m_2 #: ~m_3}

I.e. mass is an ~{absolute} quantity, not just a releative ratio between two particles. This means that we can measure mass relative to some given standard unit mass.

The accelerations induced by several particles on a particular particle are idependent of each other.

 

Force

The accelerations induced by several particles on a particular particle are idependent of each other

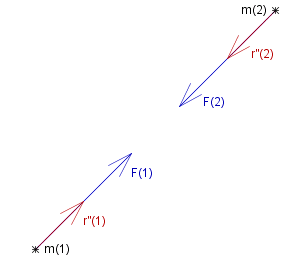
A particle with mass ~m and position #~r is said to be subject to a _ #~{force} #~F , _ where

_ _ _ #~F _ #:= _ ~m deriv2{#~r}

If particles of mass ~m_1 and ~m_2 interact causing accelerations of _ deriv2{~#r_1} _ and _ deriv2{~#r_2} _ respectively then the forces acting on them are: _ _ _ #~F_1 _ = _ ~m_1 deriv2{#~r_1} _ _ and _ _ #~F_2 _ = _ ~m_2 deriv2{#~r_2} respectively. So their ratio _ _ _ | #~F_1 | #: | #~F_2 | _ = _ ~m_1 | #~r_1 | #: ~m_2 | #~r_2 | but _ _ ~m_1 #: ~m_2 _ = _ | #~r_2 | #: | #~r_1 | _ _ => _ _ | #~F_1 | #: | #~F_2 | _ = _ 1 #: 1 i.e. _ _ | #~F_1 | _ = _ | #~F_2 | So we have Newton's 3^{rd} law: The forces acting on two particles are equal and in opposite directions.

---