Differentiation

Differentiation

h#: A --> &reals. , A &subset. &reals. , _ h continuous at ~a &in. A, _ and _ h ( ~x ) = ~x , _ &forall. ~x &in. A, ~x != ~a.
If ~a is not an isolated point then h ( ~a ) = 0.

Proof:
To be provided

f#: A --> &reals. , A &subset. &reals.. _ Let ~a be a non-isolated point of A. _ If &exist. a function f_~a^*#: A --> &reals. , _ which is continuous at ~a, and such that:
_ _ _ _ f ( ~x ) - f ( ~a ) _ = _ ( ~x - ~a ) f_~a^*( ~x ) , _ &forall. ~x &in. A ,
then we say that f is #~{differentiable} at ~a, with #~{derivative} f_~a^*( ~a ) at ~a .

The derivative, _ f_~a^*( ~a ) , _ is usually written as _ f #~' ( ~a ) _ or as _ Df ( ~a ) _.

[ In traditional terms we have f_~a^*( ~x ) _ = _ ( f ( ~x ) - f ( ~a ) ) / ( ~x - ~a ) when _ ~x != ~a,
and _ f #~' ( ~a ) _ = _ f_~a^*( ~a ) _ = _ lim_{(~x -> ~a)} f _~a^*( ~x ) _ = _ lim_{(~x -> ~a)} ( f ( ~x ) - f ( ~a ) ) / ( ~x - ~a ) ]

Uniqueness of Derivative

If it exists, the derivative of f is well defined, for if there were two functions _ f_~a^* , _ and _ f_~a^{&tilde.} _ satisfying the conditions of the definition, then put _ h _ = _ f_~a^* - f_~a^{&tilde.} _ and apply above lemma.

#{Examples};

1. f ( ~x ) _ = _ ~x^2 , _ ~x &in. &reals., _ then _ ~x^2 - ~a^2 _ = _ ( ~x - ~a )( ~x + ~a ) , _ i.e. _ f_~a^*( ~x ) _ = _ ~x + ~a , _ f #~' ( ~a ) _ = _ 2~a.
2. f ( ~x ) _ = _ 1 / ~x , _ ~x &in. &reals., ~x != 0 , _ then _ ( 1 / ~x ) - ( 1 / ~a ) _ = _ ( ~a - ~x ) / ~x~a _ i.e. _ f_~a^*( ~x ) _ = _ -1 / ~x~a , _ f #~' ( ~a ) _ = _ -1 / ~a^2.

 

 

Differentiability Implies Continuity

If _ f _ is differentiable at ~a , then f is continuous at ~a.

Proof:
To be provided

 

Derivatives of Sums and Products

If _ f _ and _ g _ are differentiable on A, then so are _ f + g , _ f g _ and _ f / g .
Furthermore

1. ( f + g )#~' ( ~a ) _ = _ f #~' ( ~a ) + g#~' ( ~a )
   _
2. ( f g )#~' ( ~a ) _ = _ f ( ~a ) g#~' ( ~a ) + f #~' ( ~a ) g ( ~a )
   _
3. ( f ./ g )#~' ( ~a ) _ = _ fract{f #~' ( ~a ) g ( ~a ) - f ( ~a ) g #~' ( ~a ), g^2 ( ~a )}

Proof:
To be provided

 

Derivative of Composition

If _ f _ is differentiable on A, and _ g _ is differentiable on f (A), _ then _ g &comp. f _ is differentiable on A, and
_ _ _ _ ( g &comp. f ) #~' ( ~a ) _ = _ g #~' ( f ( ~a ) ) . f #~' ( ~a )

 

Maxima and Minima

f#: A --> &reals. _ has a #~{local maximum} at ~a _ if _ &exist. &delta. > 0 _ such that _ f ( ~x ) =< f ( ~a ) _ &forall. ~x for which _ | ~x - ~a | < &delta. .
[ #~{local minimum} _ if _ f ( ~x ) >= f ( ~a ) _ &forall. ~x for which _ | ~x - ~a | < &delta. . ]

If _ f#: A --> &reals. _ has a local maximum or minimum at ~a , _ and _ f is differentiable at ~a , _ and _ &exist. ~r > 0 such that B( ~a, ~r ) &subset. A , _ then _ f #~' ( ~a ) = 0 .

Proof:
To be provided

 

Rolle's Theorem

If _ f#: [ ~a, ~b ] --> &reals. _ is continuous and differentiable at every point of ( ~a, ~b ) , _ and _ f ( ~a ) = f ( ~b ) , _ then _ &exist. ~c &in. ( ~a, ~b ) _ such that _ f #~' ( ~c ) = 0 .

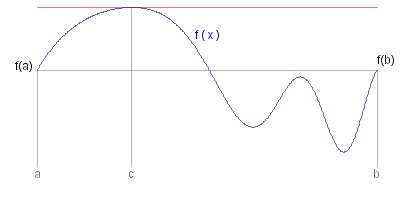
Proof:
To be provided

 

Mean Value Theorem

If _ f#: [ ~a, ~b ] --> &reals. _ is continuous and differentiable on ( ~a, ~b ) , _ then _ &exist. ~c &in. ( ~a, ~b ) _ such that _
f ( ~a ) - f ( ~b ) = ( ~b - ~a ) f #~' ( ~c ) .

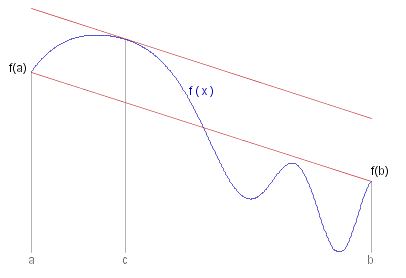
Proof:
To be provided

 

#{Corollary}:

1. f #~' ( ~x ) = 0 _ &forall. ~x &in. ( ~a, ~b ) _ => _ f _ is constant on ( ~a, ~b ) .
2. f #~' ( ~x ) > 0 _ &forall. ~x &in. ( ~a, ~b ) _ => _ f _ is strictly increasing on ( ~a, ~b ) .
3. f #~' ( ~x ) < 0 _ &forall. ~x &in. ( ~a, ~b ) _ => _ f _ is strictly decreasing on ( ~a, ~b ) .

Proof:
To be provided

 

Inverse Function Theorem

If _ f _ is a continuous surjective function _ f#: [ ~a, ~b ] --> [ &alpha., &beta. ] &subset. &reals. , _ and _ f #~' ( ~x ) > 0 , _ then _ &exist. inverse function _ g#: [ &alpha., &beta. ] --> &reals. _ which is surjective, such that _ ~y = f ( ~x ) <=> ~x = g ( ~y ) .
Moreover _ g _ is differentiable on ( &alpha., &beta. ) _ and _ g #~' ( ~y ) = 1 / f #~' ( ~x ) , _ &forall. ~y &in. ( &alpha., &beta. )

---