Inverse Square Law

Inverse Square Force

We have established the following for central forces in general:

~r ^2 deriv{&theta.} _ = _ ~h _ = _ ~{constant} deriv{~A} _ = _ ~h ./ 2 _ = _ ~{constant} ~A _ = _ ~h ~t ./ 2 + ~{integration constant} where ~A is the area swept out by #~r. fract{d ^2 ~u,d &theta. ^2} _ + _ ~u _ = _ fract{~a,~u^2 ~h ^2} where _ ~u = ~r^{-1} _ and _ ~a = | deriv2{#~r} |

We will now look at motion under a force which is inversely proportional to the distance of the particle from the origin:

| #~F | _ &propto. _ 1 ./ ~r ^2 , _ so _ ~a _ = _ &mu. ./ ~r ^2 _ (some constant &mu. > 0)

So

fract{d ^2 ~u,d &theta. ^2} _ + _ ~u _ = _ fract{&mu.,~h ^2}

This is a second order differential equation in ~u, and has auxiliary solution

~u _ = _ ~A sin &theta. + ~B cos &theta.

and a particular solution

~u _ = _ &mu. ./ ~h ^2

giving a general solution

~u _ = _ ( &mu. ./ ~h ^2 ) + ~A sin &theta. + ~B cos &theta.

which can be written

~u _ = _ ( &mu. ./ ~h ^2 ) + ~C sin &alpha. sin &theta. + ~C cos &alpha. cos &theta. _ = _ ( &mu. ./ ~h ^2 ) + ~C cos ( &theta. - &alpha. )

where _ _ ~C = &sqrt.${~A&powtwo. + ~B&powtwo.} , _ and _ &alpha. = cos^{-1} ( ~B ./ ~C ) = sin^{-1} ( ~A ./ ~C )

Note that &theta. is the angle between #~r and the ~x-axis which was arbitrarily set in the direction of the initial position of the particle. Instead we could set the ~x-axis to eliminate &alpha. i.e. set deriv{&theta.} = &theta. - &alpha. _ - _ the angle from the new ~x-axis to ~#r. So, dropping the prime, we have:

~u _ = _ ~r^{-1} _ = _ ( &mu. ./ ~h ^2 ) + ~C cos &theta.

This is the equation of a conic section, as we will show in the next section.

 

Conic Sections

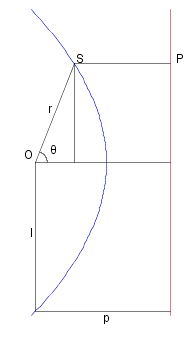Consider the diagram on the right. From the focus-directrix property of conic sections if ~e is the excentricity, we know that

~r _ = _ ~e SP _ and _ ~l _ = _ ~e ~p

but _ SP _ = _ ~p - ~r cos &theta. , _ so

~r _ = _ ~e ~p - ~e ~r cos &theta. _ = _ ~l - ~e ~r cos &theta.

~r ( 1 + ~e cos &theta. ) _ = _ ~l _ _ => _ _ ~r^{-1} _ = _ ~l ^{-1} + ~e ~l ^{-1} cos &theta.

So it can be seen that the orbital equation has the same form as this, and we can calculate the parameters of the conic section by equating coefficients, so

~l _ = _ ~h ^2 ./ &mu. , _ _ ~e _ = _ ( ~h ^2 ~C ) ./ &mu.

The form of the orbit depends on ~e:

• ~e < 1 _ _ the orbit is an elipse,
• ~e = 1 _ _ the orbit is a parabola,
• ~e > 1 _ _ the orbit is a hyperbola.

---