Integration
Step Functions
A #~{step function} is a function of the form _ &phi.#: [ ~a , ~b ] --> &reals. _ where _ ~a = ~p_0 < ~p_1 < ... < ~p_~k = ~b , _ and _ &phi. ( ~x ) = ~c_~i (constant) _ when _ ~p_{~i - 1} < ~x < ~p_~i .
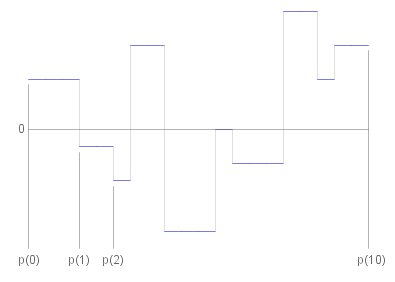
The #~{integral} of a step function is defined by:
int{&phi. ( ~x ),~a,~b,d~x} _ _ #:= _ _ sum{~c_~i ( ~p_~i - ~p_{~i - 1} ),~i = 1,~k}
This corresponds to the "area under the graph" idea of integral, where the area below the x-axis is counted as negative.
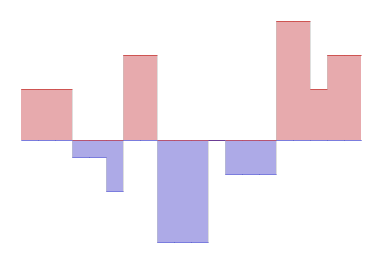
Note that the values at ~p_0, ~p_1, ... _ do not affect the value of the integral.
Also if _ ~p_{~i - 1} < ~p < ~p_~i _ any ~i, _ then _ ~c_~i ( ~p_~i - ~p_{~i - 1} ) _ = _ ~c_~i ( ~p_~i - ~p ) + ~c_~i ( ~p - ~p_{~i - 1} )
so subdivision does not affect the value of the integral.
- ~{∫}_~a^~b ( λ &phi. ( ~x ) + &mu. &psi. ( ~x ) ) d~x _ = _ λ ~{∫}_~a^~b &phi. ( ~x ) d~x + &mu. ~{∫}_~a^~b &psi. ( ~x ) d~x
- If _ &phi. ( ~x ) >= 0 _ &forall. ~x &in. ( ~a , ~b ) _ then _ ~{∫}_~a^~b &phi. ( ~x ) d~x _ >= _ 0
- If _ ~a =< ~c =< ~b _ then _ ~{∫}_~a^~b &phi. ( ~x ) d~x _ = _ ~{∫}_~a^~c &phi. ( ~x ) d~x + ~{∫}_~c^~b &phi. ( ~x ) d~x
- If _ ~m =< &phi. ( ~x ) =< ~M , _ &forall. ~x &in. [ ~a , ~b ] _ then _ ~m ( ~b - ~a ) _ =< _ ~{∫}_~a^~b &phi. ( ~x ) d~x _ =< _ ~M ( ~b - ~a )
- ~{∫}_~a^~b ( - | &phi. ( ~x ) | ) d~x _ < _ ~{∫}_~a^~b &phi. ( ~x ) d~x _ < _ ~{∫}_~a^~b | &phi. ( ~x ) | d~x
and _ | ~{∫}_~a^~b &phi. ( ~x ) d~x | _ < _ ~{∫}_~a^~b | &phi. ( ~x ) | d~x
Regulated Functions
We will develop a simple theory of integration for the following class of functions:
f#: [ ~a , ~b ] --> &reals. _ is a #~{regulated function} if &exist. a sequence of step functions \{ &phi._~n \} which converges uniformly to f on [ ~a , ~b ] .
If _ f _ is a regulated function as defined here above, _ then define its #~{integral}:
int{f ( ~x ),~a,~b,d~x} _ _ #:= _ _ lim{ int{,~a,~b,}&phi._~n ( ~x ) d~x, ~n -> &infty. }
This definition makes sense providing the following is true:
#{Lemma}: _
- ~{∫}_~a^~b &phi._~n ( ~x ) d~x _ does converge.
- If _ f ( ~x ) = lim &phi._~n ( ~x ) _ and _ f ( ~x ) = lim &psi._~n ( ~x ) _ (uniform convergence)
then _ ~{∫}_~a^~b &phi._~n ( ~x ) d~x _ and _ ~{∫}_~a^~b &psi._~n ( ~x ) d~x _ converge to the same limit.
Proof:
- Given &epsilon. > 0 , &exist. ~N _ such that _ | &phi._~n ( ~x ) - f ( ~x ) | < &epsilon. , _ &forall. ~n >= ~N, _ ~x &in. [ ~a , ~b ]
&therefore. | &phi._~m ( ~x ) - &phi._~n ( ~x ) | < 2&epsilon. , _ &forall. ~m , ~n >= ~N, _ ~x &in. [ ~a , ~b ] .
Now | ~{∫}_~a^~b &phi._~m ( ~x ) d~x - ~{∫}_~a^~b &phi._~n ( ~x ) d~x | _ =< _ ( ~b - ~a ) 2&epsilon. , _ &forall. ~m , ~n >= ~N . _ Result follows from Cauchy's General Principle of Convergence
_ - Given &epsilon. > 0 , &exist. ~N _ such that _ | &phi._~n ( ~x ) - f ( ~x ) | < &epsilon. , _ and _ | &psi._~n ( ~x ) - f ( ~x ) | < &epsilon. , _ &forall. ~n >= ~N, _ ~x &in. [ ~a , ~b ]
&therefore. | &phi._~n ( ~x ) - &psi._~n ( ~x ) | < 2&epsilon. , _ &forall. ~n >= ~N, _ ~x &in. [ ~a , ~b ] .
So _ ~{∫}_~a^~b &phi._~n ( ~x ) d~x - ~{∫}_~a^~b &psi._~n ( ~x ) d~x _ = _ ~{∫}_~a^~b ( &phi._~n ( ~x ) - &psi._~n ( ~x ) ) d~x _ -> _ 0 _ as _ ~n -> &infty. . _ So the integrals converge to the same limit.
_
The regulated functions form a vector space over &reals., _ ( i.e. _ λ ( f + g ) _ = _ λ f + λ g , _ etc., ) _ and it is fairly trivial to show that properties 1 - 3 of integrals of step functions also hold for regulated functions.
If _ f _ is a regulated function then it is bounded.
If _ &phi._~n -> f _ uniformly on [ ~a , ~b ] then &exist. ~N such that _ | f ( ~x ) - &phi._~n ( ~x ) | < 1 , _ &forall. ~x &in. [ ~a , ~b ] . _ &phi._~n _ bounded _ => _ f bounded . _
Continuous and Monotone Functions
Both continuous and monotone functions are regulated.
Proof:
- #{Continuous Functions}:
_ - #{Monotone Functions}:
_
Fundamental Theorem of Calculus
The following are two ways of expressing the idea that integration is the "reverse" of differentiation:
- If _ f _ is continuous on [ ~a , ~b ] _ and _ F ( ~x ) = ~{∫}_~a^~x f ( ~t ) d~t , _ ~x &in. [ ~a , ~b ] _ then _ F #~' ( ~x ) _ = _ f ( ~x ) , _ &forall. ~x &in. [ ~a , ~b ] .
_ - if _ F #~' ( ~x ) = f ( ~x ) _ &forall. ~x &in. [ ~a , ~b ] _ and _ f _ is continuous on [ ~a , ~b ] , _ then
_ _ _ _ _ ~{∫}_~a^~x f ( ~t ) d~t _ = _ F ( ~x ) - F ( ~a ) _ _ &forall. ~x &in. [ ~a , ~b ] .
In particular
_ _ _ _ _ ~{∫}_~a^~b f ( ~x ) d~x _ = _ F ( ~b ) - F ( ~a ) .
_
Proof:
- Suppose that _ ~c &in. [ ~a , ~b ) , _ then given _ &epsilon. > 0 , _ &exist. &delta. > 0 _ such that
_ _ _ _ _ _ ~c < ~x < ~c + &delta. _ => _ | f ( ~x ) - f ( ~c ) | < &epsilon. _ and _ ~x &in. [ ~a , ~b ] .
i.e. _ _ _ _ _ f ( ~c ) - &epsilon. _ < _ f ( ~x ) _ < _ f ( ~c ) + &epsilon. , _ &forall. ~x &in. [ ~c , ~c + &delta. ]
Then if _ 0 < ~h < &delta. ,
_F ( ~c + ~h ) - F ( ~c ) _ = _ ~{∫}_~a^{~c + ~h} f ( ~t ) d~t - ~{∫}_~a^~c f ( ~t ) d~t _ = _ ~{∫}_~c^{~c + ~h} f ( ~t ) d~t
so _ _ _ _ ~h ( f ( ~c ) - &epsilon. ) _ =< _ F ( ~c + ~h ) - F ( ~c ) _ =< _ ~h ( f ( ~c ) + &epsilon. )
[ from propery 4 , _ putting _ ~m _ = _ f ( ~c ) - &epsilon. _ and _ _ ~M _ = _ f ( ~c ) + &epsilon. ]
i.e. _ _ _ _ ( f ( ~c ) - &epsilon. ) _ =< _ ( F ( ~c + ~h ) - F ( ~c ) ) / ~h _ =< _ f ( ~c ) + &epsilon.
_ - proof to be provided
_
Integration of Products
Integration by Parts
Integration by Substitution
If _ g#: [ ~c , ~d ] --> &reals. _ has continuous derivative and if _ f _ is continuous on the interval _ I = g ( [ ~c , ~d ] ) , _ then
int{f ( ~x ) , ~a , ~b , d~x} _ _ _ = _ _ _ int{f ( g ( ~t ) ) g #~' ( ~t ), ~c , ~d , d~t}
where _ ~a = g ( ~c ) , _ ~b = g ( ~d ) .
Proof:
To be provided