Convergence of Functions
Limit of a Function
Let _ f#: A --> &reals. , _ ~a &in. A , _ ~l &in. &reals. . _ We say that _ f ( ~x ) #~{tends to} ~l #~{as} ~x #~{tends to} ~a _ if given &epsilon. > 0 , _ &exist. &delta. > 0 _ such that
| f ( ~x ) - ~l | < &epsilon. _ if _ d( ~x , ~a ) < &delta..
We also say that ~l is the #~{limit} of f ( ~x ) as ~x tends to ~a.
Write _ f ( ~x ) -> ~l _ as _ ~x -> ~a.
f#: A --> &reals. _ continuous at ~a _ <=> _ f ( ~x ) -> f(~a) _ as _ ~x -> ~a . _ This is obvious by putting ~l = f(~a) in the above definition.
#{Lemma}: _ f ( ~x ) -> ~l _ as _ ~x -> ~a , _ and _ g ( ~x ) -> ~m _ as _ ~x -> ~a , _ then
- f ( ~x ) + g ( ~x ) _ -> _ ~l + ~m _ as _ ~x -> ~a
- f ( ~x )g ( ~x ) _ -> _ ~l~m _ as _ ~x -> ~a
- providing ~m != 0 : _ f ( ~x ) / g ( ~x ) _ -> _ ~l / ~m _ as _ ~x -> ~a
Proof:
To be provided
_
_
_
Isolated Points
~a is an #~{isolated point} in A _ if _ &exist. &delta. > 0 _ such that the open ball _ B( ~a , &delta. ) = &set. ~a &xset.. _ I.e. there is an open ball that contains ~a as the only point.
#{Lemma}: _ If ~a is ~{not} an isolated point, _ then f ( ~x ) tends to at most one limit as ~x -> ~a.
Proof:
To be provided
Sequence of Functions
Pointwise Convergence
Given a sequence of functions _ &set. f_~i &xset._{~i &in. &naturals.} _ f_~i#: A --> &reals. _ and a function f#: A --> &reals.#, _ we say &set. f_~i &xset. ~#{converges pointwise} to f ( on A ) _ if _ f_~i -> f _ as _ ~n -> &infty. _ &forall. ~x &in. A.
Examples:
-
_ f_~n ( ~x ) _ = _ ~x / ~n ; _ f ( ~x ) _ = _ 0 , _ 0 =< ~x =< 1
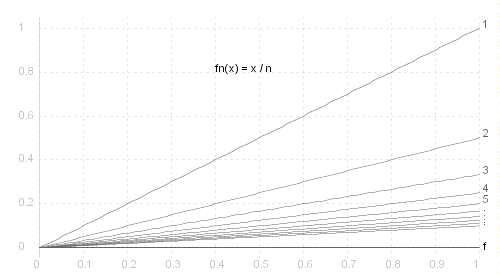
_ -
_ f_~n ( ~x ) _ = _ ~x^~n , _ 0 =< ~x =< 1 ; _ _ f ( ~x ) _ = _ array{ 0 , _ 0 =< ~x < 1 / 1 , _ ~x = 1 }
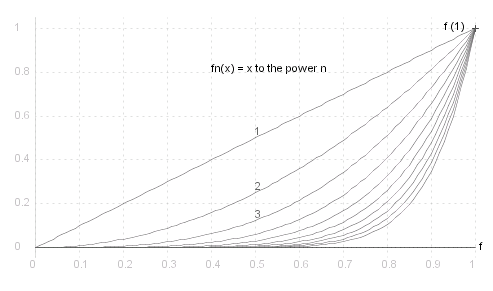
_ -
_ f_~n ( ~x ) _ = _ array{ 1 - ~n~x , _ 0 =< ~x =< 1 {/} ~n / 0, _ 1 {/} ~n < ~x =< 1} ; _ _ f ( ~x ) _ = _ array{ 1 , _ ~x = 0 / 0 , _ 0 < ~x =< 1 }
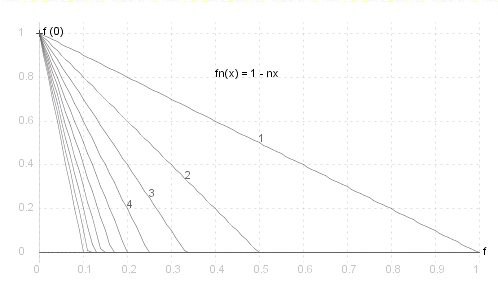
Source for the graphs shown here can be viewed by going to the diagram capture page .
Uniform Convergence
Let _ B ( A , &reals. ) _ be the set of bounded functions _ A --> &reals. , _ i.e. their range in &reals. is bounded , _ define the following metric on B ( A , &reals. ):
_ _ _ d( f , g ) _ = _ sup_{~x &in. A}( | f ( ~x ) - g ( ~x ) | )
In the above examples of pointwise convergence: _ i. _ d( f , f_~n ) = 1 / ~n ; _ ii. _ d( f , f_~n ) = 1 ; _ iii. _ d( f , f_~n ) = 1 .
&set. f_~n &xset. _ is said to ~#{converge uniformly} to f, _ if _ d( f , f_~n ) -> 0 _ as ~n -> &infty. .
I.e. given &epsilon. > 0 _ &exist. ~N > 0 _ such that _ | f_~n(~x) - f ( ~x ) | < &epsilon. , _ &forall. ~n >= ~N . _ Note that the value of ~N is independent of ~x.
Example i. above is uniformly convergent, examples ii. and iii. are not.
#{Lemma}: _ if _ f_~n is continuous &forall. ~n _ and _ f_~n -> f _ uniformly , _ then f is continuous.
Proof:
To be provided
Weirstrass' M-test
As in the case of sequences of real numbers we can construct #~{series} and #~{partial sums} of functions, put
s_~n( ~x ) _ = _ sum{f_~i ( ~x ),1,~n}
&sum._1^{&infty.} f_~i ( ~x ) _ is #~{convergent} to s( ~x ) _ if _ s_~n( ~x ) -> s( ~x ) .
&sum._1^{&infty.} f_~i ( ~x ) _ is #~{uniformly convergent} _ if _ &set. s_~n( ~x ) &xset. is uniformly convergent .
#{Theorem}: _ (#~{Weirstrass' M-test}) _ Let _ &set. ~M_~i &xset. _ be a sequence of positive real numbers such that _ &sum._1^{&infty.} ~M_~i _ is convergent, _ and _ &set. f_~i &xset. _ is a sequence of functions A --> &reals. _ such that | f_~i ( ~x ) | =< ~M_~i _ &forall. ~x and &forall. ~i.
Then _ &sum._1^{&infty.} f_~i ( ~x ) _ is uniformly (and absolutely) convergent on A.
Proof:
To be provided
#{Examples}: _
- &sum. ~x^~n _ _ uniformly convergent for _ ~x &in. [ 0, ~k ], _ 0 < ~k < 1, _ since | ~x^~n | < ~M_~n = ~k^~n _ and _ &sum. ~k^~n convergent.
- &sum. ~x^~n / ~n^2 _ _ uniformly convergent for _ ~x &in. [ -1, 1 ], _ since | ~x^~n / ~n^2 | =< ~1/~n^2 _ for | ~x | =< 1.
- &sum. ~x^~n / ~n#! _ (exponential series) _ _ uniformly convergent &forall. ~x, _ since ~x^~n / ~n#! =< ~K^~n / ~n#! _ for | ~x | < ~K _ (some ~K), _ and _ &sum. ~K^~n / ~n#! _ is convergent, _ so _ &sum. ~x^~n / ~n#! _ uniformly convergent on [ -~K, ~K ] _ for any ~K, _ let ~K -> &infty.
Power Series
If the power series _ &sum. ~a_~n ~x^~n _ has a radius of convergence R, _ then it is continuous at every point ~p , _ | ~p | < R.
Proof:
given _ ~p , _ | ~p | < R. _ Select ~k such that | ~p | =< ~k < R , _ ~k > 0. _ So _ &sum._~n^{&infty.}_{= 0} _ | ~a_~n | ~k^~n convergent (by absolute convergence). _ Let ~M_~n = | ~a_~n | ~k^~n . _ So _ &sum. ~a_~n ~x^~n _ uniformly convergent by Weirstrass, _ &therefore. the sum is continuous at ~p .