Logarithmic function

Integral of Reciprocal

Define the function L#: ( 0 , &infty. ) --> &reals. _ by

L ( ~x ) _ = _ int{,1,~x,}fract{1,~t} d~t _ _ _ _ ~x > 0

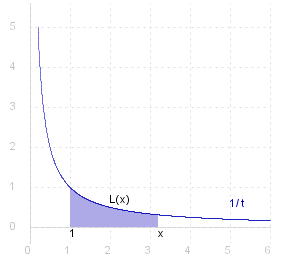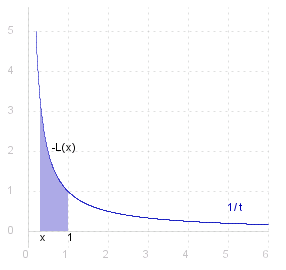~x >= 1	~x < 1 [ by convention _ ~{∫}_~b^~a f ( ~t ) d~t _ = _ - ~{∫}_~a^~b f ( ~t ) d~t ]

L#~' ( ~x ) _ = _ ( 1 / ~x ) _ _ _ ( by the fundamental theorem ). _ L ( 1 ) _ = _ 0 , _ _ L ( 2 ) > 1/2 , _ _ L ( 3 ) > {1/2} + 1/3 = 5/6, _ etc.

L ( ~x~y ) = L ( ~x ) + L ( ~y ) , _ _ &forall. ~x , ~y > 0
since _ _ _ ~{∫}_1^{~x~y} ( 1 / ~t ) d~t _ = _ ~{∫}_1^{~x} ( 1 / ~t ) d~t + ~{∫}_~x^{~x~y} ( 1 / ~t ) d~t _ _ _ ( ~y >= 1 )
_ _ _ _ _ _ _ ~{∫}_1^{~x} ( 1 / ~t ) d~t _ = _ ~{∫}_1^{~x~y} ( 1 / ~t ) d~t + ~{∫}_{~x~y}^~x ( 1 / ~t ) d~t _ _ _ ( ~y < 1 )
_ _ _ _ _ _ => _ ~{∫}_1^{~x~y} ( 1 / ~t ) d~t _ = _ ~{∫}_1^{~x} ( 1 / ~t ) d~t + ~{∫}_~x^{~x~y} ( 1 / ~t ) d~t
and _ _ _ _ ~{∫}_~x^{~x~y} ( 1 / ~t ) d~t _ = _ ~{∫}_1^{~y} ( 1 / ~u ) d~u _ = _ L ( ~y )
[ using substitution _ ~x~u = ~t _ d~t = ~x d~u , _ 1 / ~t = 1 / ~x~u , _ ~u = 1 _ <=> _ ~t = ~x , _ ~u = ~y _ <=> _ ~t = ~x~y ]
In particular: _ _ L ( 2^~n ) _ = _ L ( 2 ) + L ( 2 ) + ... + L ( 2 ) _ = _ ~n L ( 2 ) _ > _ ~n / 2

So L is a continuous strictly increasing function, unbounded above. _ Hence _ L ( ~x ) -> &infty. _ as _ ~x -> &infty..

Now _ L ( 1 / ~x ) _ = _ - L ( ~x ) , _ so _ L ( ~x ) -> -&infty. _ as _ ~x -> 0

So _ D ( L ( ~x ) ) = 1 / ~x, _ but we have seen that D ( log ~x ) _ = _ 1 / ~x , _ i.e. _ D ( L ( ~x ) - log ~x ) _ = _ 0 _ => _ L ( ~x ) - log ~x = ~c _ (constant). _ But _ ~c = 0 _ (evaluating for ~x = 1), _ so

~{∫}_1^~x ( 1 / ~t ) d~t _ == _ log ~x

 

Exponential as Limit of Sequence

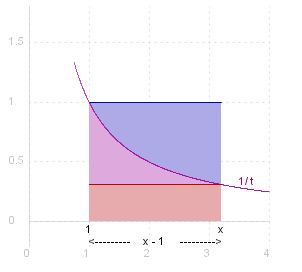
As can be seen from the diagram, _ ( ~x - 1 ) / ~x _ =< _ log ~x _ =< _ ~x - 1 , _ _ ~x >= 1
For _ ~x < 1 , _ ~x - 1 _ =< _ - log ~x _ =< _ ( ~x - 1 ) / ~x , _ _ which gives the same result, which therefore holds &forall. ~x > 0.

( ~x - 1 ) / ~x _ =< _ log ~x _ =< _ ~x - 1 , _ _ &forall. ~x >= 0

Putting _ ~x _ = _ ( 1 + ( ~y / ~n ) )

fract{ _ ~y / ~n , 1 + ( ~y / ~n )} _ _ =< _ _ log rndb{ 1 + fract{ ~y , ~n }} _ _ =< _ _ fract{ ~y , ~n }

or

fract{ _ ~y _ , 1 + ( ~y / ~n )} _ _ =< _ _ ~n log rndb{ 1 + fract{ ~y , ~n }} _ _ =< _ _ _ ~y

The lower bound _ -> _ ~y , _ _ as _ ~n -> &infty.. _ So

_ _ _ _ log ( 1 + ( ~y / ~n) )^~n _ -> _ ~y , _ _ as _ ~n -> &infty.

taking the exponential of both sides:

( 1 + ( ~y / ~n) )^~n _ -> _ exp ~y , _ _ as _ ~n -> &infty.

Arithmetic and Geometric Mean

Let _ \{ ~a_1 , ... , ~a_~n \} _ be a set of ~n positive real numbers (not necessarily distinct). _ The #~{arithmetic mean} of these numbers is defined to be _ ( &sum. ~a_~i ) / ~n. _ _ Their #~{geometric mean} is defined to be _ ^~n&sqrt.( &prod. ~a_~i ) .

Putting _ ~A _ = _ ( &sum. ~a_~i ) / ~n , _ and _ ~G _ = _ ^~n&sqrt.( &prod. ~a_~i ) , _ from the result that _ log ~x =< ~x - 1 _ we have
_ _ _ _ log ( ~a_1 / ~A ) _ =< _ ( ~a_1 / ~A ) - 1
_ _ _ _ log ( ~a_2 / ~A ) _ =< _ ( ~a_2 / ~A ) - 1
_ _ _ _ ... _ _ _ ... _ _ _ ...
_ _ _ _ log ( ~a_~n / ~A ) _ =< _ ( ~a_~n / ~A ) - 1
adding:
_ _ _ _ log ( ~a_1 ~a_2 ... ~a_~n / ~A^~n ) _ =< _ ( ~a_1 + ~a_2 + ... + ~a_~n / ~A ) - ~n _ = _ ( ~n~A / ~A ) - ~n _ = _ 0 .
i.e.
_ _ _ _ log ( ~G^~n / ~A^~n ) _ =< _ 0 _ => _ log ( ~G / ~A ) _ =< _ 0 .
So

~G _ =< _ ~A

Euler's Constant

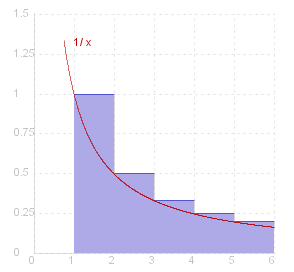
Clearly _ log ~n _ < _ 1 + {1/2} + 1/3 + ... + 1 / ( ~n - 1 ) . _ Now put _ ~s_~n _ = _ 1 + {1/2} + 1/3 + ... + 1 / ~n _ - _ log ~n . _ Then _ ~s_~n _ > _ 1 / ~n _ > _ 0 .

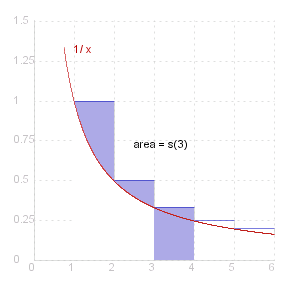
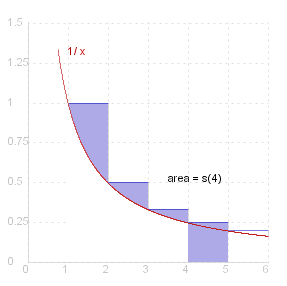
Now _ ~s_{~n + 1} - ~s_~n _ = _ 1 / ( ~n + 1 ) _ - _ log ( ( ~n + 1 ) / ~n ) _ =< _ 1 / ( ~n + 1 ) _ - _ ~n^2 / ( ~n + 1 ) _ = _ 1 - ~n _ < _ 0 _ ( ~n > 1 )

So _ \{ ~s_~n \} _ is a decreasing sequence of positive terms, and converges to a limit known as #~{Euler's constant} _ ( &gamma. = 0.577 ... ) .
&gamma. = &sum._1^{&infty.} ( 1/~n - ( log ( ~n + 1 ) - log ( ~n ) )

Log 2

fract{1,~n + 1} + fract{1,~n + 2} + ... + fract{1,2~n} _ = _ ~s_{2~n} - ~s_~n + log 2~n - log ~n

_ _ _ _ _ _ _ _ _ _ --> _ _ &gamma. - &gamma. + log 2 _ = _ log 2 , _ _ as ~n -> &infty.

Maclaurin expansion for _ log ( 1 + ~x ):

log ( 1 + ~x ) _ = _ ~x - fract{~x^2,2} + fract{~x^3,3} - fract{~x^4,4} + ... _ _ for | ~x | < 1

This gives a series expansion for log ~y , _ where _ 0 < ~y < 2. _ Can we obtain an expansion for ~y = 2 ,_ i.e. for log ( 1 + ~x ) , _ where _ ~x = 1 ?
Consider the Taylor expansion for 1 / ( 1 + ~x ) about 0:

fract{1,1 + ~x} _ = _ 1 - ~x + ~x^2 - ~x^3 + ... + ({-1})^~n~x^~n _ + _ fract{( -~x )^{~n + 1},( 1 + &theta.~x )^{~n + 2}}

where _ 0 < &theta. < 1 .

Now

int{,0,1,}fract{1,1 + ~x} d~x _ = _ script{sqrb{log ( 1 + ~x )},,,1,0} _ = _ log 2

So

log 2 _ = _ int{,0,1,}fract{1,1 + ~x} d~x _ = _ script{sqrb{~x - fract{~x^2,2} + fract{~x^3,3} ... fract{({-1})^~n~x^{~n + 1},~n + 1 }},,,1,0} + int{,0,1,}fract{( -~x )^{~n + 1},( 1 + &theta.~x )^{~n + 2}} d~x

_ = _ 1 - fract{1,2} + fract{1,3} ... fract{({-1})^~n,~n + 1 } + int{,0,1,}fract{( -~x )^{~n + 1},( 1 + &theta.~x )^{~n + 2}} d~x

Now the denominator in the remainder term , _ ( 1 + &theta.~x )^{~n + 2} _ =< _ 1 , _ since ( 1 + &theta.~x ) _ =< _ 1 , _ &forall. 0 < ~x < 1 . _ So

int{,0,1,}fract{( -~x )^{~n + 1},( 1 + &theta.~x )^{~n + 2}} d~x _ _ =< _ _ int{,0,1,}( -~x )^{~n + 1} d~x

_ = _ script{sqrb{fract{( -1)( -~x )^{~n + 2},~n + 2}},,,1,0} _ = _ fract{( -1)^{~n + 3},~n + 2} _ _ -> _ _ 0 , _ as ~n -> &infty.

So the remainder term disapears as _ ~n -> &infty., so we can write

log 2 _ = _ 1 - fract{1,2} + fract{1,3} - ... _ = _ sum{fract{({-1})^~r,~r + 1 },0,&infty.}

And so

log ( 1 + ~x ) _ = _ ~x - fract{~x^2,2} + fract{~x^3,3} - fract{~x^4,4} + ... _ _ for _ -1 < ~x =< 1

---