Bases and Components

Linear Independence

A set of vectors, \{ #~a_1 , ... , #~a_~n \} is said to be #~{linearly dependent} if &exist. scalars \{ λ_1 , ... , λ_~n \}, not all zero, such that :

sum{ λ_~i #~a_~i , 1, ~n} _ = _ 0

I.e. at least one of the vectors (one for which the corresponding scalar is not zero), it can be expressed as a linear sum of the other vectors.

If the set of vectors is not linearly dependent it is said to be #~{linearly independent}. I.e. a set of vectors is linearly independent if no one of them can be expressed as a linear sum of the others.

Obviously a set containing a single non-zero vector \{ #~a \} is linearly independent. A set of two non-zero vectors \{ #~a , #~b \} is linearly independent if there is no non-zero λ such that #~a = λ#~b, i.e. ~#a and #~b are not colinear (have the same or opposite direction).

If #~a and #~b are linearly independent non-zero vectors (i.e. not colinear) then what about \{ #~a , #~b , #~c \}, where #~c is also non-zero?
If _ #~c = &mu. #~a + λ #~b , _ i.e. the set is linearly dependent, then ~#c is in the plane defined by ~#a and #~b. If #~c is not coplanar with #~a and #~b then it cannot be expressed as such a linear sum.

Dimension

The ~{maximum} number of vectors that can be linearly independent is three. This number is called the #~{dimension} of the vector space.

(In the general theory , vector spaces can have any dimension, but here we restrict our iterest to vectors in ~{three dimensional} real space, &reals.^3.)

Any set of three linearly independent non-zero vectors #~{spans} the vector space, i.e. any vector can be expressed as a linear sum of these three vectors. The set is therefore said to form a #~{basis} for the space.

Given a basis for &reals.^3, \{ #~v_1, #~v_2, #~v_3 \}, say, then any vector #~a can be represented as a linear sum of these three vectors:

#~a _ = _ ~a_1 #~v_1 + ~a_2 #~v_2 + ~a_3 #~v_3,

In fact the numbers ~a_1, ~a_2, ~a_3, are unique, since if _ #~a _ = _ ~a'_1 #~v_1 + ~a'_2 #~v_2 + ~a'_3 #~v_3, _
then

( ~a_1 - ~a'_1 ) #~v_1 + ( ~a_2 - ~a'_2 ) #~v_2 + ( ~a_3 - ~a'_3 ) #~v_3 _ = _ #0

_ - _ contradicting linear independence, unless ~a_1 = ~a'_1, _ etc.

The numbers ~a_1, ~a_2, ~a_3, are called the #~{co-ordinates} of #~a with respect to the basis \{ #~v_1, #~v_2, #~v_3 \}

Rectangular Coordinates

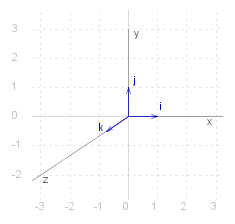
A special basis is the #~{right-handed orthonormal} basis formed by the three unit vectors, #~i, #~j, and #~k, where the angle between #~i and #~j is a right angle ( &pi. ./ 2 radians ) and #~k is normal to the plane defined by #~i and #~j, such that if you rotate counter-clockwise through &pi. ./ 2 radians ~{from} #~i ~{to} #~j, then #~k is in the direction upwards out of the plane. Conventionally ~#i, #~j, and #~k lie along the ~x-, ~y-, and ~z-axes in the three dimensional Cartesian space, as shown in the diagram. Any vector can then be represented as #~a _ = ~a_~x ~#i + ~a_~y #~j + ~a_~z #~k ~a_~x, ~a_~y, and ~a_~z are known as the #~{rectangular coordinates} of the vector.

If _ #~a _ = ~a_~x ~#i + ~a_~y #~j + ~a_~z #~k _ and _ #~b _ = ~b_~x ~#i + ~b_~y #~j + ~b_~z #~k _ then

• | #~a | _ = _ &sqrt.(~a_~x ^2 + ~a_~y ^2 + ~a_~z ^2)
• λ #~a _ = _ λ ~a_~x ~#i + λ ~a_~y #~j + λ ~a_~z #~k
• #~a + #~b _ = _ ( ~a_~x + ~b_~x ) ~#i + ( ~a_~y + ~b_~y ) #~j + ( ~a_~z + ~b_~z ) #~k

 

 

---