Oscillations

Springs

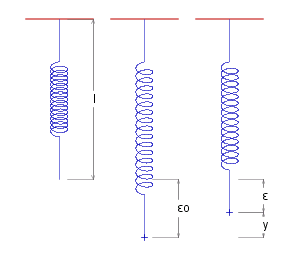
Consider a spring suspended from a point. Suppose that the length of the unstretched spring is ~l and that its mass is negligible.

_

#~{Hooke's Law} states that the force exerted by a spring is proportional to the amount it is stretched.

If we now attach a particle of mass ~m to the end of the spring, the force exerted by the spring on the particle is ~k&epsilon., where ~k is a constant called the #~{stiffness} of the spring, and &epsilon. is the distance the spring has been extended. This force will be in an upward (positive) direction, and will be counteracted by the force of gravity, ~m~g , in a downward direction.

So total force acting on particle will be

~F _ = _ ~k&epsilon. - ~m~g

The forces will balance exactly when the spring is extended a certain length, &epsilon._0 say. So

&epsilon._0 _ = _ ~m ~g ./ ~k

We will (arbitrarily) set the origin at this point of equilibrium, and let ~y measure the distance of the particle from this point (in an upward direction). So

~y _ = _ &epsilon._0 - &epsilon. _ _ => _ _ ~F _ = _ ~k ( &epsilon._0 - ~y ) - ~m~g _ = _ -~k~y _ _ => _ _ ~m ~y'' + ~k~y _ = _ 0

~y'' + &omega.^2~y _ = _ 0 , _ _ where _ &omega. = &sqrt.${~k ./ ~m}

Simple Harmonic Motion

The equation of motion

~y'' + &omega.^2~y _ = _ 0

has a solution

~y _ = _ ~C cos &omega.~t + ~D sin &omega.~t

(see Calculus notes on Orinary Differential Equations: Second Order Homogenous Equations .)

This can be written:

~y _ = _ ~A sin ( &omega.~t + &phi. ) , _ _ where _ ~A = &sqrt.${ ~C&powtwo. + ~D&powtwo. } , _ and _ &phi. = sin^{-1} ( ~C ./ ~A )

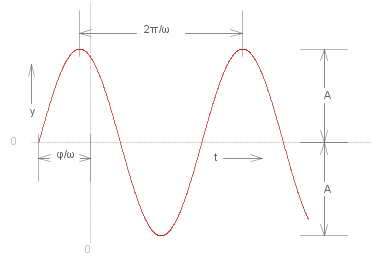~A is called the #~{amplitude} , _ &omega. is known as the #~{angular frequency} , _ and &phi. is called the ~#{phase}. The graph for ~y is shown (right) with some of these quantities illustrated.

Note that this is (of course) a periodic function, which repeats every 2&pi./&omega. time units. This constitutes one #~{cycle} of the oscillation. This means that there are &omega./2&pi. cycles per time unit, this is known as the #~{frequency} of the oscillation. If the frequency is denoted by ~f, then

~f _ #:= _ &omega./2&pi. , _ _ _ ~y _ = _ ~A sin ( 2&pi.~f~t + &phi. )

There is a lot of information on the web about Simple Harmonic Motion. See for example, HyperPhysics , hosted by the Department of Physics and Astronomy at Georgia State University.

Damped Oscillations

Suppose that in addition to the force towards the point of equilibrium, which is proportional to the distance from the point, there is a frictional force proportional to the velocity of the particle (and in the opposite direction).

~F _ = _ -~k~y - ~q~y'

Giving an equation of motion:

~y'' + 2&beta. ~y' + &gamma.^2 ~y _ = _ 0 , _ _ _ where _ &beta. = ~q ./ 2~m > and _ &gamma. = &sqrt.${ ~k ./ ~m }

If _ &gamma.&powtwo. > &beta.&powtwo. _ ( 4~m~k&powtwo. > ~q ) _ then this has a solution :

~y _ = _ ~e^{-&beta.~t} ~A sin ( ~t &sqrt.${ &gamma.&powtwo. - &beta.&powtwo. } + &phi. )

where _ A _ and _ &phi. _ are arbitrary constants. _ Put &omega. = &sqrt.${ &gamma.&powtwo. - &beta.&powtwo. } _ and the solution becomes:

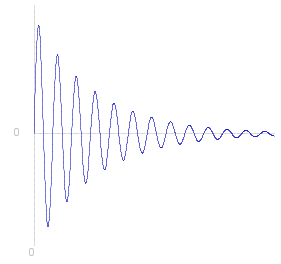
~y _ = _ ~e^{-&beta.~t} ~A sin ( &omega.~t + &phi. )

So this has the same (initial) amplitude and angular frequency as the non-damped oscillation, but the amplitude decreases exponentially (see diagram right).

_

_

If _ &gamma.&powtwo. < &beta.&powtwo. _ ( 4~m~k&powtwo. < ~q ) _ then the solution is:

~y _ = _ ~A exp \{ ~t ( - &beta. + &sqrt.${ &beta.&powtwo. - &gamma.&powtwo. } ) \} + ~B exp \{ ~t ( - &beta. - &sqrt.${ &beta.&powtwo. - &gamma.&powtwo. } ) \}

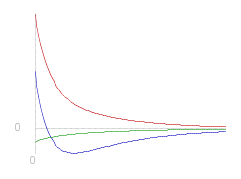
Note that as _ &beta. > &sqrt.${ &beta.&powtwo. - &gamma.&powtwo. } _ both exponents will be negative, and therefore the expression is the sum of two exponentially decreasing components.

There can be at most one turning point in such a function. Three examples are shown (left) where the arbitrary constants are the only difference in each case (same ~q and ~k etc.)

_

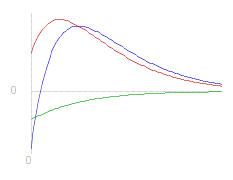If _ &gamma.&powtwo. = &beta.&powtwo. _ ( 4~m~k&powtwo. = ~q ) _ then the solution is:

~y _ = _ ~A exp \{ - &beta. ~t \} + ~B ~t exp \{ - &beta. ~t \}

Motion is said to be ~#{critically damped} or ~#{dead beat}.

There can be at most one turning point. Examples with different arbitrary constants are shown in the graph on the right.

_

_

---