Elipse
Elipse Geometry
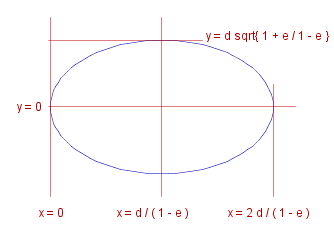
As we have seen previously , the equation for an elipse can be written:
_ _ ~y^2 _ = _ 2 ~d ( 1 + ~e ) ~x - ( 1 - ~e^2 ) ~x^2 _ _ _ ~d >= 0 , _ 0 =< ~e =< 1
[Note: we write ~d instead of ~a in this form of the equation, as conventionally ~a represents another parameter with respect to an elipse, as we shall see below.]
~y is defined in the range _ 0 =< ~x =< 2~d ./ ( 1 - ~e ) . _ The curve is obviously symmetric about ~y = 0, i.e. about the ~x-axis. It is not difficult to show that it is also symmetric about the line ~x = ~d ./ ( 1 - ~e ) . Note that at _ ~x = ~d ./ ( 1 - ~e ) ,
~y = +- d fract{&sqrt.${1 + ~e},&sqrt.${1 - ~e}}
Elipse Equation
We will now show a simpler equation for the elipse. We'll do this by moving the curve by ~d ./ ( 1 - ~e ) to the left, i.e. so that the "centre" of the elipse co-incides with the origin.
~y^2 _ = _ 2 ~d ( 1 + ~e ) rndb{ ~x + fract{~d,1 - ~e} } _ - _ ( 1 - ~e^2 ) script{rndb{ ~x + fract{~d,1 - ~e} },,, 2,}
_ _ _ _ = _ 2 ~d _ fract{1 + ~e,1 - ~e} ( ( 1 - ~e ) ~x + ~d ) _ - _ fract{1 + ~e,1 - ~e}( ( 1 - ~e ) ~x + ~d )^2
_ _ _ _ = _ fract{1 + ~e,1 - ~e} ( 2 ~d ( 1 - ~e ) ~x + 2 ~d ^2 - (1 - ~e)^2 ~x^2 - ~d ^2 - 2 ~d (1 - ~e) ~x )
_ _ _ _ = _ fract{1 + ~e,1 - ~e} ( ~d ^2 - ( 1 - ~e )^2 ~x^2 )
so
( 1 - ~e )^2 ~x^2 + fract{1 - ~e,1 + ~e} ~y^2 _ = _ ~d ^2
which can be written
|
fract{~x^2,~a^2} + fract{~y^2,~b^2} _ = _ 1 |
where
~a^2 _ = _ fract{~d ^2,( 1 - ~e )^2 } , _ and _ ~b^2 _ = _ fract{~d ^2 ( 1 + ~e ),1 - ~e}
Dimensions
Note that ~a is just half the length of the elipse, and is known as the #~{semi major axis} of the elipse, while ~b is half the height, and known as the #~{semi minor axis}.
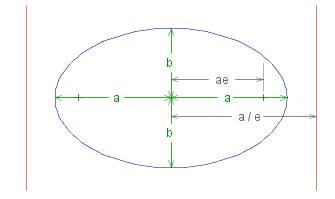
The original parameters can be expressed in terms of ~a and ~b:
fract{~b^2,~a^2} _ = _ ( 1 + ~e )( 1 - ~e ) _ = _ ( 1 - ~e^2 )
=> _ _ ~e _ = _ script{rndb{1 - fract{~b&powtwo.,~a&powtwo.}},,, 1/2 ,}
~d _ = _ ~a ( 1 - ~e )
Note also that as the elipse is symmetric about ~x = 0 , there is a second focus at _ ~x = ~e ~a , _ ~y = 0 . The directrices will be at ~d ./ ~e from the edges of the elipse, i.e. at _ ~a + ( ~a ( 1 - ~e ) ./ ~e ) _ = _ ~a ./ ~e _ from the centre.
Parametric Equation
Consider any point ~P ( ~x , ~y ) on the elipse. Draw a vertical line from the ~x-axis through ~P to the circle, radius ~a, encircling the elipse. Then draw a line from this point on the circle to the common centre of the elipse and the circle. Let the angle between this last line and the ~x-axis be &phi..
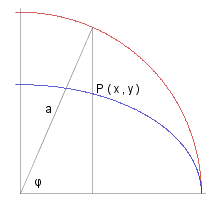
_ _ _ ~x _ = _ ~a cos &phi.
_ _ _ ~y^2 _ = _ ~b^2 ( 1 - ( ~x^2 / ~a^2 ) ) _ = _ ~b^2 ( 1 - cos^2 &phi. )
_ _ _ _ _ = _ ~b^2 sin^2 &phi.
| ~x _ = _ ~a cos &phi. ~y _ = _ ~b sin &phi. |
Inter Focal Triangle
Consider an elipse with the focii at the points R and S as shown in the diagram below. Then for any point P ( ~x , ~y ) on the elipse (for illustration we show P in the top right-hand quadrant of the elipse, but the following result holds for the other quadrants by symmetry):
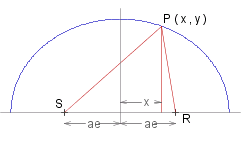
SP^2 _ = _ ( ~a~e + ~x )^2 + ~y^2 _ = _ ~a^2~e^2 + ~x^2 + ~y^2 + 2~a~e~x
but _ ~a^2~e^2 _ = _ ~a^2 ( 1 - ( ~b^2 ./ ~a^2 ) ) _ = _ ~a^2 - ~b^2
and _ ~y^2 _ = _ ~b^2 ( 1 - ( ~x^2 ./ ~a^2 ) ) _ = _ ~b^2 - ( ~b^2~x^2 ./ ~a^2 )
so _ _ SP^2 _ = _ ~a^2 + ~x^2 - ( ~b^2~x^2 ./ ~a^2 ) + 2~a~e~x _ = _ ~a^2 + ~e^2~x^2 + 2~a~e~x
Similarly _ _ RP^2 _ = _ ( ~a~e - ~x )^2 + ~y^2 _ = _ ~a^2 + ~e^2~x^2 - 2~a~e~x
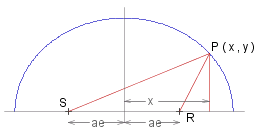
Note that if _ ~x > ~a~e , _ as in the diagram on the right, then
RP^2 _ = _ ( ~x - ~a~e )^2 + ~y^2 , _ _ which is the same.
Now _ _ ( SP + RP )^2 _ = _ SP^2 + RP^2 + 2 SP.RP
_ _ _ = 2( ~a&powtwo. + ~e&powtwo.~x&powtwo. ) + 2 &sqrt.${ ( ~a&powtwo. + ~e&powtwo.~x&powtwo. )&powtwo. - 4 ~a&powtwo.~e&powtwo.~x&powtwo. }
_ _ _ = 2( ~a&powtwo. + ~e&powtwo.~x&powtwo. ) + 2 &sqrt.${ ( ~a&powtwo. - ~e&powtwo.~x&powtwo. )&powtwo. } _ = _ 2~a
So _ SP + RP _ = _ ~a &sqrt.$2 , _ _ for any point P on the elipse. This is a mathematical justification of the method of drawing an elipse by pinning each end of a piece of string at the focii, and keeping the string taught with the pencil to draw the elipse.
Source for the graphs shown here can be viewed by going to the diagram capture page .