Helix Geometry

Helix Tangent

The diagram is of a helix, which has the vector representation #~r(&phi.) _ = _ 3 cos &phi. #~i - 3 sin &phi. #~j + 4 &phi. #~k Now d#~r ./ d&phi. _ = _ - 3 sin &phi. #~i - 3 cos &phi. #~j + 4 #~k |d#~r ./ d&phi.|^2 _ = _ 9 sin^2 &phi. + 9 cos^2 &phi. + 16 |d#~r ./ d&phi.| _ = _ &sqrt.${ 9 + 16 } _ = _ 5 So the tangent vector #~t _ = _ - 3/5 sin &phi. #~i - 3/5 cos &phi. #~j + 4/5 #~k Note |~#t| _ = _ &sqrt.${ 9/25 + 16/25 } _ = _ 1 d#~t ./ d&phi. _ = _ - 3/5 cos &phi. #~i + 3/5 sin &phi. #~j |d#~t ./ d&phi.|^2 _ = _ 9/25 cos^2 &phi. + 9/25 sin^2 &phi. |d#~t ./ d&phi.| _ = _ 3/5

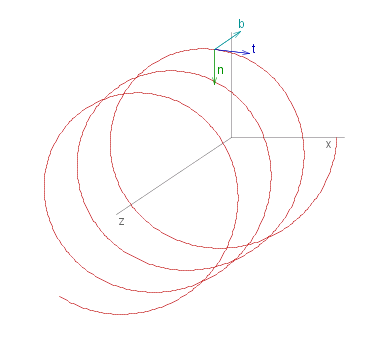Helix Curvature and Radius

So the curvature: _ _ &kappa. _ = _ |d#~t ./ d&phi.| -: |d#~r ./ d&phi.| _ = _ 3/25

giving a radius of: _ _ &rho. _ = _ 25/3 _ = _ 8.33333...

Note that in reality the helix is much more stretched than the impression given by the diagram, had the helix had the equation

#~r(&phi.) _ = _ 3 cos &phi. #~i - 3 sin &phi. #~j + &phi. #~k

instead, the curvature, &kappa., would be 3/10, and the radius, &rho., would be 3.33333... , not much greater than the radius of the enveloping cylinder, i.e. 3.

Helix Normal and Binormal

We can now calculate _ #~n:

#~n _ = _ d#~t ./ d&phi. -: |d#~t ./ d&phi.| _ = _ - cos &phi. #~i + sin &phi. #~j

and _ #~b:

#~b _ = _ #~t # #~n _ = _ ( - 3/5 sin &phi. #~i - 3/5 cos &phi. #~j + 4/5 #~k ) _ # _ ( - cos &phi. #~i + sin &phi. #~j )

_ _ _ _ = _ ( - 4/5 sin &phi. ) #~i _ + _ ( - 4/5 cos &phi. ) #~j _ + _ ( - 3/5 sin^2 &phi. - 3/5 cos^2 &phi. ) #~k

_ _ _ _ = _ - 1/5 ( 4 sin &phi. #~i _ + _ 4 cos &phi. #~j _ + _ 3 #~k )

now

d#~b ./ d&phi. _ = _ - 4/5 cos &phi. #~i + 4/5 sin &phi. #~j

so

d#~b ./ d~s _ = _ d#~b ./ d&phi. -: |d#~r ./ d&phi.| _ = _ - 4/25 cos &phi. #~i + 4/25 sin &phi. #~j _ = _ 4/25 #~n

Giving the torsion of the helix as a constant _ _ &tau. _ = _ -4/25.

---