Gravity

Gravitational Force

Two particles with mass ~m_1 and ~m_2 and position ~#r_1 and ~#r_2 respectively, exert a #~{gravitational} force of attraction on each other, whose magnitude is

fract{&gamma. ~m_1 ~m_2, | #~r_1 - #~r_2 | ^2}

where _ &gamma. _ is the #~{universal gravitational constant}.

The sum of gravitational forces acting on a particle can be regarded as a vector field. The force acting on a particle in a gravitational field is known as the partic;es ~#{weight}, which should not be confused with it's mass.

Earth's Mass

We assume that the Earth is a uniform sphere of radius ~r, in which case we can regard its mass, _ ~m_E , _ as a point mass at the centre. The force of gravity acting on the particle of mass ~m is therefore | #~F | _ = _ fract{&gamma. ~m ~m_E, _ ~r ^2} but _ _ #~F _ = _ ~m ~#g , _ _ where #~g is the acceleration due to gravity at the Earth's surface, so

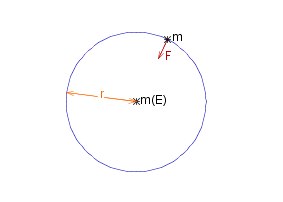~m | #~g | _ = _ fract{&gamma. ~m ~m_E, _ ~r ^2} _ _ => _ _ | #~g | _ = _ fract{&gamma. ~m_E, _ ~r ^2} _ _ => _ _ ~m_E _ = _ fract{ | #~g | ~r ^2,&gamma.}

Note in the central equation that #~g is independent of the mass ~m - as demonstrated by Galileo, reportedly by dropping cannon balls of different masses from the Leaning Tower of Pisa.

The quantities | #~g |, ~r, and &gamma. can be established by experimental observation:

| #~g | = 9.8 ms^{-1} , _ ~r = 6.38 # 10^{6} m , _ &gamma. = 6.67 # 10^{6} m^3s^{-1}k^{-1}

=> _ _ ~m_E _ = _ 5.98 # 10^{24} k.

---