Continuous Random Variables

Distribution Function

Recall that if _ ~X #: ( &Omega. , @A ) --> ( &reals. , @B ), _ is a random variable then the c.d.f. of ~X is given by: _ _ F( ~c ) _ = _ P( ~X =< ~c ) .

F is non-decreasing and right continuous. We saw in the case of discrete random variables that F need not be continuous (i.e. left-continuous) and can be non-increasing (i.e. constant) over some intervals.

A random variable is said to be a #~{continuous random variable} if its distribution function is continuous.

Density Function

If ~X is a random variable with distribution function F_~X , and &exist. a function f_~X #: &reals. --> &reals.^+ , _ such that

F_~X ( ~c ) _ = _ int{,{-&infty.},~c,} f_~X ( ~t ) d~t

for any ~c &in. &reals. , _ then f_~X is called the #~{probability density function} (#~{p.d.f.}) of the distribution.

Not all random variables have a density function, but all the ~{"well behaved"} continuous ones do, and in such cases the distribution is often characterized by the density function.

Example: Normal Distribution

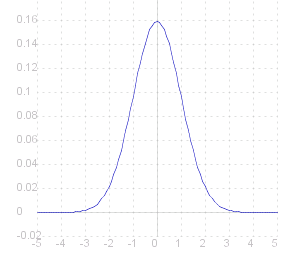
One of the most commonly met examples of a contiuous random variable is the Normal Distribution . This is actually a family of distributions with the p.g.f. differing depending on a couple of parameters. Here we give as an example the ~{standard normal distribution} whose p.g.f. is

f( ~x ) _ = _ fract{1,&sqrt.${2&pi.}} e ^{- ~x^2/2 }

The graph of which looks like this:

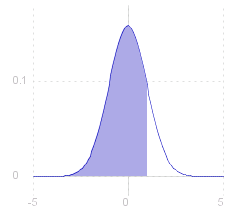
The probability that the value of the random variable is less than a given value, ~c, is given by the distribution function, F( ~c ) : F( ~c ) _ = _ fract{1,&sqrt.${2&pi.}} int{,{-&infty.},~c,} e ^{- ~x^2/2 } _ d~x This is shown (right) as the area under the graph of the p.g.f. ( where ~c = 1 ).

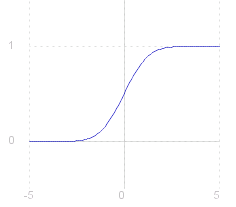
The distribution function (c.d.f.) of the normal distribution cannot be given as an explicit function, but only as an integral (above). To calculate the distribution for specific values of ~c, the student has recourse to printed statistical tables, such as Neave , or to computer packages such as the Look-up facility on this site. The graph of the distribution function for the standard normal distribution is shown (right).

Details of the normal and other continuous random variables are given in Appendix 2: Continuous Distributions .

Expectation

If ~X is a random variable, and the density function f_~X exist; , then the #~{expectation} or #~{mean} of ~X is given by

E( ~X ) _ = _ int{,{-&infty.},{+&infty.},} ~t f_~X ( ~t ) d~t

Example:
For the standard normal distribution introduced above, the expectation is

E( ~X ) _ = _ fract{1,&sqrt.${2&pi.}} int{,{-&infty.},&infty.,} ~x e ^{- ~x^2/2 } _ d~x

but note that the function _ g( ~x ) _ = _ ~x e ^{- ~x^2/2 } _ is anti-symmetric about 0, i.e. _ g( -~x ) _ = _ - g( ~x ) . _ So

int{,{-&infty.},0,} ~x e ^{- ~x^2/2 } _ d~x _ = _ - int{,0,&infty.,} ~x e ^{- ~x^2/2 } _ d~x

and

int{,{-&infty.},&infty.,} ~x e ^{- ~x^2/2 } _ d~x _ = _ int{,{-&infty.},0,} ~x e ^{- ~x^2/2 } _ d~x _ + _ int{,0,&infty.,} ~x e ^{- ~x^2/2 } _ d~x _ = _ 0

So we have that the mean of a variable with the standard normal distribution is zero.

Variance

As for discrete random variables , if ~X is a random variable and ~X ^2 has finite expectation, then we define the #~{variance}:

var( ~X ) _ = _ &sigma.^2 _ = _ E( [ ~X - E( ~X ) ]^2 ) _ = _ E( ~X ^2 ) - E( ~X )^2

Actual calculations can be done when we have looked at the distribution of the square of a random variable .

---