Complex Numbers

Imaginary Numbers

It's well known that he solution of a simple quadratic equation _ ~{ax}^2 + ~{bx} + ~c = 0 _ is given by:

~x _ = _ fract{-~b +- &sqrt.${ ~b&powtwo. - 4~a~c },2~a}

However this will only give a "real" solution if _ ~b&powtwo. >= 4~a~c , _ otherwise the solution is

~x _ = _ fract{-~b _ +- _ &sqrt.${ 4~a~c - ~b&powtwo. } _ &sqrt.${ -1 },2~a}

and _ &sqrt.${ -1 } _ doesn't exist amongst the real numbers. We get around this by defining the number _ ~i _ #:= _ &sqrt.${ -1 } . _ Any number of the form _ ~a ~i , _ where ~a is a real number, is said to be an #~{imaginary} number.

Complex Numbers

A number of the form _ ~z _ = _ ~a + ~i ~b , _ where ~a and ~b are real numbers and _ ~i _ #:= _ &sqrt.${ -1 } , _ is called a #~{complex} number.

The #~{real part} of ~z is definded _ @R ( ~z ) _ #:= _ ~a , _ and the #~{imaginary part} of ~z is definded _ @I ( ~z ) _ #:= _ ~b . _ Note that both @R ( ~z ) and @I ( ~z ) are real numbers.

Given the algebraic properties of ~i ( i.e. _ ~i ^2 = -1 ), we can define the following operations:

Let _ ~z_1 _ = _ ~a + ~i ~b , _ and _ ~z_2 _ = _ ~c + ~i ~d

addition:

~z_1 + ~z_2 _ = _ ( ~a + ~c ) + ~i ( ~b + ~d )

subtraction:

~z_1 - ~z_2 _ = _ ( ~a - ~c ) + ~i ( ~b - ~d )

multiplication:

~z_1 # ~z_2 _ = _ ( ~a~c - ~b~d ) + ~i ( ~a~d + ~b~c )

Before defining division, it will be useful to define the following quantities, given _ ~z_1 _ = _ ~a + ~i ~b :

_ _ _ _ the #~{modulus} of ~z , _ | ~z | _ #:= _ &sqrt.${ ~a&powtwo. + ~b&powtwo. }

_ _ _ _ the #~{complex conjugate} of ~z , _ $~z _ #:= _ ~a - ~i ~b

Note that _ ~z $~z _ = _ ~a^2 + ~b^2 + ~i ( ~a~b - ~b~a) _ = _ | ~z |^2 , _ we can use this to define division of complex numbers:

~z_1 -: ~z_2 _ = _ fract{~z_1 $~z_2,~z_2 $~z_2} _ = _ fract{( ~a~c + ~b~d ),~c^2 + ~d ^2} + ~i fract{ ( ~b~c - ~a~d ),~c^2 + ~d ^2}

Argand Diagram

Let ~z be a complex number _ _ ~z _ = _ ~x + ~i ~y , _ _ ~x, ~y &in. &reals. , _ ~i ^2 = -1

A complex number can be represented by a pair ( ~x, ~y ) of real numbers. We can therefore associate a complex number with a point in two-dimensional Cartesian plane (see diagram).

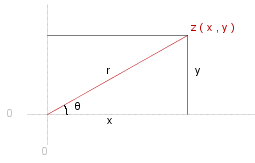
Define the following quantities

• &theta. _ = _ tan^{-1}( ~y ./ ~x ) _ _ _ is called the #~{argument} of ~z, written _ arg ( ~z ).
• _
• ~r _ = _ &sqrt.${~x&powtwo. + ~y&powtwo.} _ _ _ is called the #~{modulus} of ~z, written _ mod ( ~z ).

Note that _ ~x _ = _ ~r cos &theta. , _ ~y _ = _ ~r sin &theta. . So we can now represent ~z by _ _

~z _ = _ ~r ( cos &theta. + ~i sin &theta. )

Note that if _ ~z _ = _ ~r ( cos &theta. + ~i sin &theta. ) _ then ~z _ = _ ~r ( cos &theta. + ~i sin ( &theta. + 2~n&pi. ) ) , _ for any whole number ~n. To make the representation unique we restrict the value of &theta. to _ -&pi. =< &theta. =< +&pi.. This is called the #~{principal value} of the argument of ~z, and is denoted _ Arg ( ~z ).

Exponential Function

For real ~x

exp ~x _ = _ sum{fract{~x^~n,~n#!},~n = 0,&infty.} _ = _ 1 + ~x + fract{~x^2,2#!} + fract{~x^3,3#!} + ...

cos ~x _ = _ sum{fract{-1^~n ~x^{2~n},2~n#!},~n = 0,&infty.} _ = _ 1 - fract{~x^2,2#!} + fract{~x^4,4#!} - fract{~x^6,6#!} + ...

sin ~x _ = _ sum{fract{-1^~n ~x^{2~n + 1},(2~n + 1)#!},~n = 0,&infty.} _ = _ ~x - fract{~x^3,3#!} + fract{~x^5,5#!} - fract{~x^7,7#!} + ...

which motivate the following definitions, in all cases ~x is a real number:

exp ~i~x _ = _ sum{fract{(~i~x)^~n,~n#!},~n = 0,&infty.} _ = _ 1 + ~i ~x - fract{~x^2,2#!} - ~ifract{~x^3,3#!} + fract{~x^4,4#!} + ...

cos ~i~x _ = _ sum{fract{-1^~n (~i~x)^{2~n},2~n#!},~n = 0,&infty.} _ = _ 1 + fract{~x^2,2#!} + fract{~x^4,4#!} + fract{~x^6,6#!} + ...

sin ~i~x _ = _ sum{fract{-1^~n (~i~x)^{2~n + 1},(2~n + 1)#!},~n = 0,&infty.} _ = _ ~i ~x + ~i fract{~x^3,3#!} + ~i fract{~x^5,5#!} + ~i fract{~x^7,7#!} + ...

Note that

~e^{~i~x} _ #:= _ exp ~i~x _ = _ cos ~x + ~i sin ~x

But _ _ ~z _ = _ ~r ( cos &theta. + ~i sin &theta. ) , _ where ~r is the modulus, and &theta. is the argument of ~z. So ~z can be represented

~z _ = _ ~r ~e^{ ~i&theta.}

Note also that

_ _ _ _ _ _ cos ~i~x - ~i sin ~i~x _ = _ exp ~x

Functions of a Complex Number

Let ~z be the complex number _ _ ~z _ = _ ~x + ~i ~y

_ _ _ _ ~e ^~z _ = _ ~e ^{~x + ~i ~y} _ = _ ~e ^~x ~e ^{~i ~y} _ = _ ~e ^~x ( cos ~y + ~i sin ~y )

---