Product of Vectors

1 Scalar Product

If a and b are two vectors with an angle θ between them, then we define their scalar product or dot product, denoted a · b is the real number given by:

• a · b ...= ...| a | | b | cos θ

The following are fairly obvious:

• b · a ...= ...a · b
• ( λ a ) · b ...= ...λ ( a · b )

a · b = 0 ...⇔ ...a = 0 or b = 0 or cos θ = 0. ...Cos θ = 0 if a and b are perpendicular, so we have, for ...a ≠ 0, b ≠ 0 :

• a · b = 0 ...⇔ ...a ┴ b

The following also hold for scalar product:

• a · ( b + c ) ...= ...a · b + a · c;

1.1 Scalar Product by Coordinates

If ...a ...= ...a_x i + a_y j + a_z k ...and ...b ...= ...b_x i + b_y j + b_z k, ...then

a · b ...= ...( a_x i + a_y j + a_z k ) · ( b_x i + b_y j + b_z k )

...............= ...a_x b_x + a_y b_y + a_z b_z

since ......i · i = j · j = k · k = 1 and ......i · j = j · i = j · k = k · j = k · i = i · k = 0

2 Vector Product

If a and b are two vectors with an angle θ between them, then we define their vector product or cross product, denoted a × b is the vector for which: .........| a × b | ...= ...| a | | b | sin θ a × b being at right angles to both a and b, such that a, b, c form a right handed set, i.e. if the angle θ is anti-clockwise from a to b, in the plane of a and b, then a × b is upwards out of the plane, like the direction of a conventional screw (see diagram).

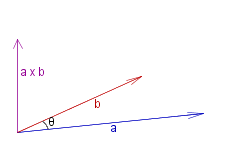We have

• b × a ...= ...– a × b
• ( λ a ) × b ...= ...λ ( a × b )

The magnitude ...| a | | b | sin θ ...represents the area of the parallelogram with a and b as two of its sides.

2.1 Vector Product by Coordinates

If ...a ...= ...a_x i + a_y j + a_z k ...and ...b ...= ...b_x i + b_y j + b_z k, ...then

a × b ...= ...( a_x i + a_y j + a_z k ) × ( b_x i + b_y j + b_z k )

...............= ...a_x b_y k – a_x b_z j – a_y b_x k a_y b_z i + a_z b_x j – a_z b_y i

...............= ...(a_y b_z – a_z b_y ) i + (a_z b_x – a_x b_z) j + (a_x b_y – a_y b_x ) k

since ......i × i = j × j = k × k = 0 and ......i × j = k, ...j × i = –k, ...j × k = i, ...k × j = –i, ...k × i = j, ...i × k = –j

This can be written

a × b ...= ...

│ │ │

i j k ax ay az bx by bz

│ │ │

3 Scalar Triple Product

The quantity ( a × b ) · c is called the scalar triple product of a, b, and c.

Suppose a, b, c form a right-handed set i.e. the angle between c and a × b is acute, φ say. Now | a × b | is the area of the parallelogram with a and b as two sides, and ...| c | cos φ ...is the height of the parallelopied with sides a b and c. So the volume of the parallelopied is:

......base × height ...= ...| a × b | | c | cos φ ...= ...( a × b ) · c

Now c, a, b is also a right-handed set, forming the same parallelopied, and so by symmetry:

......volume ...= ...( a × b ) · c ...= ...( c × a ) · b ...= ...( b × c ) · a

and by commutativity of the scalar product these are also equal to:

..................= ...c · ( a × b )...= ...b · ( c × a )...= ...a · ( b × c )

So the scalar triple product of any even permutation of a, b, and c is the same. We denote this quantity by ...[ a, b, c ].

Since ...a × b ...= ...– b × a ...then ...[ a, b, c ] ...= ...– [ b, a, c ] , ...etc.

4 Vector Triple Product

( a × b ) × c is called a vector triple product of a, b, and c. We will show that, in general ...( a × b ) × c ...≠ ...a × ( b × c )

( a × b ) × c ...is perpendicular to both ( a × b ) and c. In particular, as it is perpendicular to ( a × b ) then it must lie in the plane of a and b, i.e ...( a × b ) × c ...= ...λ a + μ b , ...some λ, μ ∊ IR

Now ...(( a × b ) × c ) · c ...= ...[ ( a × b ), c , c ] ...= ...0 , ...so ...λ (a · c) + μ (b · c) ...= ...0 ...⇒ ...λ ...= ...– μ (b · c) ⁄ (a · c)
i.e. ...( a × b ) × c ...= ...μ ( b – ( (b · c) ⁄ (a · c) ) a )

Put ...( a × b ) × c ...= ...K_c ( (a · c) b – (b · c) a ) .........where ...K_c ...= ...μ ⁄ (a · c) ............... (1)

In particular ...( a × b ) × a ...= ...K_a ( (a · a) b – (b · a) a )
So ...( a × b ) × a · b ...= ...K_a ( (a · a) b · b – (b · a) a · b )
.........( a × b ) · ( a × b ) ...= ...K_a ( a ² b ² – (a · b) ² )
.........a ² b ² sin ² θ ...= ...K_a a ² b ² ( 1 – cos ² θ )
......⇒ ...K_a = 1 ...⇒ ...( a × b ) × a ...= ...(a · a) b – (b · a) a ............... (2)

From (1) ⋯ ...( a × b ) × c · a ...= ...K_c ( (a · c) b · a – (b · c) a · a )
but ...( a × b ) × c · a ...= ...[ ( a × b ), c, a ] ...= ...– [ ( a × b ), a, c ] ...= ...– ( a × b ) × a · c ...= ...– (a · a) b · c + (b · a) a · c ......(from (2)) ⇒ ...K_c = 1 ...for any c, ...which gives us the result

( a × b ) × c ...= ...(a · c) b – (b · c) a

Note that ...a × ( b × c ) ...= ...– ( b × c ) × a ...= ...(a · c) b – (a · b) c

---