Motion
Uniform Gravitational Field
|
We want to investigate the motion of a particle of mass ~m in a uniform gravitational field, where the acceleration due to gravity is ~g. The position of the particle is given by the position vector ~#r, its initial position is #~a and its initial velocity is #~u, at time ~t = 0. Let #~k be the unit vector in the opposite sense to the gravitational force. ( In everyday terms #~k would be the unit vector vertically upwards ). Then ~m deriv2{#~r} _ = _ - ~m ~g #~k _ _ or _ _ deriv2{#~r} _ = _ - ~g #~k Integrating with respect to time ~t deriv{#~r} _ = _ - ~g #~k ~t + #~c_1 , _ _ where _ #~c_1 _ is constant. Using the initial conditions _ deriv{#~r} ( 0 ) _ = _ #~u , _ we get _ #~c_1 = #~u , _ i.e. deriv{#~r} _ = _ #~u - ~g #~k ~t |
 |
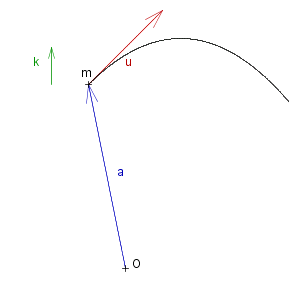 |
Integrating again with respect to ~t #~r _ = _ #~u ~t - ~g #~k ~t^2 + #~c_2 , _ _ where _ #~c_2 _ is constant. and since _ ~#r ( 0 ) _ = _ #~a _ we get #~r _ = _ #~a + #~u ~t - ~g #~k ~t^2 I.e. the path traced by the particle is a parabola in the plane of #~u and #~k . |
Energy in a Gravitational Field
|
We saw that _ ~m deriv2{#~r} _ = _ - ~m ~g #~k . _ Take scalar product with _ deriv{#~r} ~m deriv{#~r} &dot. deriv2{#~r} _ = _ - ~m ~g deriv{#~r} &dot. #~k Integrating &hlf. ~m deriv{#~r}^2 _ = _ - ~m ~g #~r &dot. #~k + #~c_3 , _ _ #~c_3 constant. Through initial conditions we have _ #~c_3 _ = _ &hlf. ~m #~u^2 + ~m ~g #~a &dot. #~k , so the kinetic energy of the particle is given by ~T _ = _ &hlf. ~m #~u^2 - ~m ~g ( #~r - #~a ) &dot. #~k |
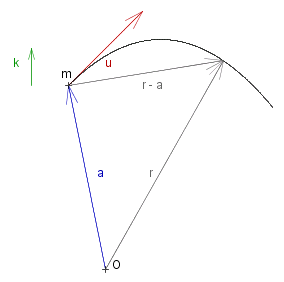 |
Note that the quantity _ ~m ~g ( #~r - #~a ) &dot. #~k _ is zero at time ~t = 0, positive so long as #~r - #~a is above the horizontal, negative below the horizontal.
So the kinetic energy of the particle is initially _ &hlf. ~m #~u^2 , _ at first it decreases and then increases until the particle is at the same 'height' as when it started, at which point it has the same kinetic energy as initially (and therefore the same velocity - though in a different direction), and then increases indefinitely.
So _ _ ~T ( ~t ) - ~T ( 0 ) _ = _ - ~m ~g ( #~r - #~a ) &dot. #~k . _ We can now substitute for #~r from the previous section to get an expression for the kinetic energy difference in terms of the time passed:
_ _ _ = _ - ~m ~g ( #~a + #~u ~t - ~g #~k ~t^2 - #~a ) &dot. #~k _ _ _ = _ - ~m ~g ( #~u ~t - ~g #~k ~t^2 ) &dot. #~k
_ _ _ = _ - ~m ~g (( #~u &dot. #~k ) ~t - ~g ~t^2 ) _ _ _ = _ ~m ( ~g ~t )^2 - ~m ~u cos &theta. ~g ~t
where _ ~u _ = _ | #~u | , _ and _ &theta. _ is the angle between the initial trajectory ( #~u ) and the vertical ( #~k ).
Resistance
We now introduce an element of resistance into the above situation. Suppose the resistive force is _ - λ ~m deriv{#~r}
~m deriv2{#~r} _ = _ - ~m ~g #~k - λ ~m deriv{#~r}_ _ or _ _ deriv2{#~r} _ = _ - ~g #~k - λ deriv{#~r}
Integrating with respect to time ~t
deriv{#~r} _ = _ - ~g #~k ~t - λ #~r + #~c_4 , _ _ where _ #~c_4 _ is constant.
Using the initial conditions _ deriv{#~r} ( 0 ) _ = _ #~u , _ #~r(0) _ = _ #~a , _ we get _ #~c_4 = #~u + λ #~a , _ i.e.
deriv{#~r} _ = _ #~u + λ ( #~a - #~r ) - ~g #~k ~t
I.e this is a first order differential equation:
deriv{#~r} + λ #~r + ~g #~k ~t - #~u - λ #~a _ = _ 0
Source for the graphs shown on this page can be viewed by going to the diagram capture page .