Forced Oscillations

Forced Undamped Oscillations

Suppose that a particle in simple harmonic motion is subject to an additional periodically varying force, called the #~{exciter}

~F _ = ~T sin ( &omega._1 ~t ) , _ where _ ~T and &omega._1 are constants.

So the equation of motion is now inhomogenous:

deriv2{~y} + &omega.^2~y _ = _ ( ~T / ~m ) sin ( &omega._1 ~t )

The complementary function is the solution for the simple harmonic motion :

~y _ = _ ~A sin ( &omega.~t + &phi. )

To find the particular integral (P.I.), consider _ ~z _ = _ ~x + ~i~y , _ where ~y is P.I. of the above equation, and ~x is the P.I. of

deriv2{~x} + &omega.^2~x _ = _ ( ~T / ~m ) cos ( &omega._1 ~t )

then if we can find a ~z which is the P.I. of

deriv2{~z} + &omega.^2~z _ = _ ( ~T / ~m ) [ cos ( &omega._1 ~t ) + ~i sin ( &omega._1 ~t ) ]

_ = _ ( ~T / ~m ) exp \{ ~i ( &omega._1 ~t ) \}

then we can calculate ~y, as _ ~y _ = _ @I ( ~z )

It is easy to show that _ ~z _ = _ ~C exp\{ ~i &omega._1 ~t \} _ is a solution of the equation, where

~C _ = _ fract{~T,~m} fract{exp\{ ~i &omega._1 ~t \},( &omega.^2 - &omega._1^2 )}

So using @I ( ~z ) as the P.I. for ~y, the general solution is

~y _ = _ fract{~T,~m} fract{sin ( &omega._1 ~t ),( &omega.^2 - &omega._1^2 )} + ~A sin ( &omega.~t + &phi. )

Providing _ &omega._1 != &omega. . _ For the case where _ &omega._1 = &omega. _ see Resonance below

To demonstrate, we determine ~A and &phi. for the initial conditions where the particle is at rest at time zero, i.e.

~y ( 0 ) _ = _ ~A sin &phi. _ = _ 0 _ _ => _ _ &phi. = 0 , 2&pi. ... ( 2~n&pi. )

deriv{~y} _ = _ fract{~T,~m} fract{&omega._1 cos ( &omega._1 ~t ),( &omega.^2 - &omega._1^2 )} + &omega. ~A cos ( &omega.~t + &phi. )

deriv{~y} ( 0 ) _ = _ fract{~T,~m} fract{&omega._1,( &omega.^2 - &omega._1^2 )} + &omega. ~A _ = _ 0

So

~A _ = _ - fract{~T,~m &omega.} fract{&omega._1,( &omega.^2 - &omega._1^2 )}

and in this case:

~y ( ~t ) _ = _ fract{~T,~m ( &omega.^2 - &omega._1^2 )} rndb{sin ( &omega._1 ~t ) - fract{&omega._1,&omega.} sin ( &omega.~t )}

_

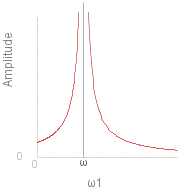
The expression involving sines in brackets on the right can vary between +- ( 1 + &omega._1/&omega.) so the amplitude of the resulting oscillation will be:

mod{fract{~T,~m ( &omega.^2 - &omega._1^2 )} fract{&omega. + &omega._1,&omega.}} _ = _ mod{fract{~T,~m &omega. ( &omega. - &omega._1 )}}

The graph on the right shows how amplitude will vary with &omega._1, the angular frequency of the exciter

Note that the solution can also be written:

~y ( ~t ) _ = _ fract{~T, &omega.~m } rndb{fract{ &omega. sin ( &omega._1 ~t ) - &omega._1 sin ( &omega.~t ),( &omega.^2 - &omega._1^2 )}}

Resonance

Above we found the particular integral (P.I) for the equation

deriv2{~z} + &omega.^2~z _ = _ ( ~T / ~m ) exp \{ ~i ( &omega._1 ~t ) \}

When _ &omega._1 = &omega. _ the particular integral found above for ~z is not sufficient (it adds nothing to the complementary function). So in this case try a solution of the form _

~z _ = _ ~C ~t e^{ ~i&omega.~t }

Solving for C we get:

~C _ = _ fract{~T,2~m&omega.~i}

and the P.I. for ~z is

~z _ = _ fract{~T,2~m&omega.~i}~t e^{ ~i&omega.~t } _ = _ fract{~T ~t,2~m&omega.~i} ( cos( &omega.~t ) + ~i sin( &omega.~t ) )

Taking the imaginary part as the P.I. for ~y, the general solution is

~y ( ~t ) _ = _ ~A sin( &omega.~t + &phi.) - fract{~T ~t,2~m&omega.} cos( &omega.~t )

differentiating:

deriv{~y} ( ~t ) _ = _ ~A &omega. cos( &omega.~t + &phi.) - fract{~T,2~m&omega.} ( cos( &omega.~t ) - &omega.~t sin( &omega.~t ) )

So with the same initial conditions as before ( ~y ( 0 ) = 0 , _ deriv{~y} ( 0 ) = 0 ), we have

&phi. _ = _ 0, ... 2~n&pi., _ _ ~A _ = _ fract{~T,2~m&omega.^2}

~y ( ~t ) _ = _ fract{~T,2~m&omega.^2} ( sin( &omega.~t ) - &omega.~t cos( &omega.~t ) )

The ~t term in the last expression ensures that the amplitude of ~y will increase without limit.

 

 

---

Below is a series of graphs that show the oscillations for different values of &omega._1, compared to the unforced oscillations of the particle (first graph). The last graph is the case of resonance.

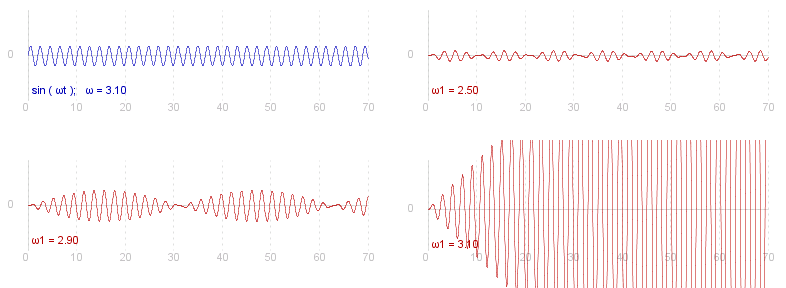
For an excellent simulation of forced oscillations see Walter Fendt's Web Page at www.walter-fendt.de/ph14e/resonance.htm .

Forced Damped Oscillations

Suppose we have oscillations that are both forced and damped due to friction, the equation of motion becomes:

deriv2{~y} + 2&beta. deriv{~y} + &gamma.^2 ~y _ = _ ( ~T / ~m ) sin ( &omega._1 ~t )

The complementary function is the solution for the unforced damped motion :

~y _ = _ ~e^{-&beta.~t} ~A sin ( &omega.~t + &phi. ), _ _ _ _ ( &gamma.^2 > &beta.^2 )

~y _ = _ ~A exp \{ ~t ( - &beta. + &sqrt.${ &beta.&powtwo. - &gamma.&powtwo. } ) \} + ~B exp \{ ~t ( - &beta. - &sqrt.${ &beta.&powtwo. - &gamma.&powtwo. } ) \}, _ _ _ _ ( &gamma.^2 < &beta.^2 )

~y _ = _ ~A exp \{ - &beta. ~t \} + ~B ~t exp \{ - &beta. ~t \}, _ _ _ _ _ _ _ _ ( &gamma.^2 = &beta.^2 )

For the P.I. of the equation we will find the P.I. of the complex eqation

deriv2{~z} + 2&beta. deriv{~z} + &gamma.^2 ~z _ = _ ( ~T / ~m ) exp \{ ~i &omega._1 ~t \}

and take the imaginary part for ~y. _ Try _ ~z = ~C exp \{ ~i &omega._1 ~t \} , _ then by taking derivatives we get

( - &omega._1^2 + 2&beta. ~i &omega._1 + &gamma.^2 ) ~C exp \{ ~i &omega._1 ~t \} _ = _ ( ~T / ~m ) exp \{ ~i &omega._1 ~t \}

 

~C _ = _ fract{~T,~m ( &gamma.^2 - &omega._1^2 + 2&beta. ~i &omega._1 )} _ = _ fract{~T ( &gamma.^2 - &omega._1^2 - 2&beta. ~i &omega._1 ), ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )}

~z _ = _ fract{~T,~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )} ( &gamma.^2 - &omega._1^2 - 2&beta. ~i &omega._1 ) exp \{ ~i &omega._1 ~t \}

Now

( &gamma.^2 - &omega._1^2 - 2&beta. ~i &omega._1 ) exp \{ ~i &omega._1 ~t \} _ = _ ( &gamma.^2 - &omega._1^2 - 2&beta. ~i &omega._1 ) ( cos ( &omega._1 ~t ) + ~i sin ( &omega._1 ~t ) )

The imaginary part of which is

( &gamma.^2 - &omega._1^2 ) sin ( &omega._1 ~t ) - 2&beta. &omega._1 cos ( &omega._1 ~t ) _ = _ ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 } sin ( &omega._1 ~t + &psi.)

where _

&psi. _ = _ cos^{-1} rndb{fract{&gamma.^2 - &omega._1^2, ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 } }}

So the P.I. is

~y _ = _ fract{~T sin ( &omega._1 ~t + &psi.), ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }}

The general solution will depend on the relative values of _ &beta. #:= ~q/2~m , _ and _ &gamma. #:= &sqrt.${~k/~m} , _ where ~k is the stiffness of the spring, and ~q is the coefficient of friction.

We will look at the case where &gamma.^2 > &beta.^2. _ The general solution is:

~y ( ~t ) _ = _ ~e^{-&beta.~t} ~A sin ( &omega.~t + &phi. ) + fract{~T sin ( &omega._1 ~t + &psi.), ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }}

where _ &omega. = &sqrt.${&gamma.&powtwo. - &beta.&powtwo.} . _ As before we will consider the initial conditions _ ~y ( 0 ) = 0 _ and deriv{~y} ( 0 ) = 0.

deriv{~y} ( ~t ) _ = _ ~e^{-&beta.~t} ~A ( &omega. cos ( &omega.~t + &phi. ) - &beta. sin ( &omega.~t + &phi. ) ) + fract{ &omega._1 ~T cos ( &omega._1 ~t + &psi. ), ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }}

~y ( 0 ) _ = _ 0 _ _ =>

~A sin &phi. _ = _ fract{- ~T sin &psi., ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }}

deriv{~y} ( 0 ) _ = _ 0 _ _ =>

&omega. ~A cos &phi. - &beta. ~A sin &phi. + fract{ &omega._1 ~T cos &psi., ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }} _ = _ 0

&omega. ~A cos &phi. + fract{~T ( &beta. sin &psi. + &omega._1 cos &psi. ), ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }} _ = _ 0

~A cos &phi. _ = _ fract{ - ~T ( &beta. sin &psi. + &omega._1 cos &psi. ), &omega. ~m ( ( &gamma.^2 - &omega._1^2 )^2 + 4 &beta.^2 &omega._1^2 )^{ 1/2 }}

tan &phi. _ = _ fract{ &omega. sin &psi., &beta. sin &psi. + &omega._1 cos &psi. } _ = _ fract{ &omega. , &beta. + &omega._1 cot &psi. }

---