Intermediate Value Theorem

Intermediate Value Theorem

#{Theorem}: _ f#: [ ~a, ~b ] --> &reals. continuous, then

1. The range of f is bounded.
2. The range of f contains a least member, &alpha. say, and a greatest member, &beta. say.
3. f ( ~a ) =< &gamma. =< f ( ~b ) _ => _ &gamma. &in. f [ ~a, ~b ]. _ i.e _ &gamma. = f ( ~c ), some ~c &in. [ ~a,~b ]. _ (#~{Intermediate value theorem} .)

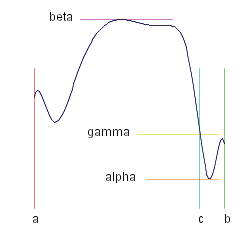
Bounded Functions

We say that f is #~{bounded} on [ ~a, ~b ] if the range of f is bounded.
So the first part of the theorem says that a continuous functions is bounded.

#{Proof of Theorem}:
To be provided

1. 
   _
2. 
   _
3. 
   _

Intermediate Value Corollaries

f#: [ ~a, ~b ] --> &reals., _ f continuous on [ ~a, ~b ] , _ then the range of _ f _ is a closed interval [ ~{&alpha.}, ~{&beta.} ] &subseteq. &reals.

f continuous on [ ~a, ~b ] _ and _ f ( ~a ) , f ( ~b ) _ have opposite signs, _ then the equation _ f ( ~x ) = 0 _ has at least one solution in [ ~a, ~b ]

f continuous on [ ~a, ~b ] _ with range _ [ ~{&alpha.}, ~{&beta.} ] , _ then if _ f _ is strictly increasing, it has a continuous, strictly increasing inverse function, _
g#: [ ~{&alpha.}, ~{&beta.} ] --> &reals. , _ with range [ ~a, ~b ].

---