Algebraic Structures
Cartesian Product
If A and B are sets, their #~{Cartesian product} , _ A # B , _ is the set of ordered pairs: _ \{ ( ~a, ~b ) | ~a &in. A , ~b &in. B \}
An ordered pair is such that _ ( ~a, ~b ) = ( ~a#~', ~b#~' ) _ <=> _ ~a = ~a#~' and ~b = ~b#~'. _ So _ ( ~a, ~b ) != ( ~b, ~a ) _ unless A = B and ~a = ~b.
Binary Operations
An (internal) #~{binary operation} on a set S is a mapping _ &theta. #: S # S -> S.
For example, if _ S = \{ ~s, ~t \}, then &theta. #: S # S -> S defined by: _ ( ~s, ~s )&theta. = ~s , _ ( ~s, ~t )&theta. = ~s , _ ( ~t, ~s )&theta. = ~t , _ ( ~t, ~t )&theta. = ~s , _ is a binary operation.
If S has ~n elements then S # S has ~n^2 elements, and so there are ~n^{~n^2} different binary operations on S.
For a binary operation _ &theta. #: S # S -> S, it is usual to denote the image _ ( ~s, ~t )&theta. _ by _ ~s &comp. ~t , _ ~s + ~t , _ or _ ~s~t. _ A binary operation denoted by _ ~s + ~t _ is called addition, one denoted by _ ~s~t _ is called multiplication, though at this stage there is no essential difference between the two.
A binary operation on a finite set is conveniently specified in a table. So for the example above
| _ | ~s | ~t |
| ~s | ~s | ~s |
| ~t | ~t | ~s |
Or more generally:
| _ | ~a | ~b |
| ~a | ~a~a | ~a~b |
| ~b | ~b~a | ~b~b |
Most algebraic structures consist of one set with one or more binary operations, subject to various restrictions (axioms).
Fields
Let S be a set with two binary operations: multiplication, denoted ~a~b, and addition, denote ~a + ~b.
S is called a field (with these operations) if they satisfy the following:
| Associative Laws: _ _ &forall. ~a, ~b, ~c &in. S: | |||||
| _ | A1. | ( ~a + ~b ) + ~c _ = _ ~a + ( ~b + ~c ) | _ _ | M1. | ( ~a~b ) ~c _ = _ ~a ( ~b~c ) |
| Commutative Laws: _ _ &forall. ~a, ~b &in. S: | |||||
| _ | A2. | ~a + ~b _ = _ ~b + ~a | _ _ | M2. | ~a~b _ = ~b~a |
| Identity Laws: _ _ &forall. ~a &in. S: | |||||
| _ | A3. | &exist. 0 &in. S such that _ _ 0 + ~a = ~a + 0 = ~a |
_ _ | M3. | &exist. 1 &in. S such that _ _ 1~a = ~a1 = ~a |
| Inverse Laws: | |||||
| _ | A4. | &forall. ~a &in. S, &exist. -~a &in. S, such that _ _ ~a + -~a = -~a + ~a = 0 |
_ _ | M4. | &forall. ~a &in. S, ~a != 0, &exist. ~a^{-1} &in. S, such that _ _ ~a~a^{-1} = ~a^{-1}~a = 1 |
| Distributive Laws: _ _ &forall. ~a, ~b, ~c &in. S: | |||||
| _ | D1. | ~a ( ~b + ~c ) _ = _ ~a~b + ~a~c | |||
| _ | D2. | ( ~b + ~c ) ~a _ = _ ~b~a + ~c~a | |||
A field is the most restrictive general algebraic structure with two internal binary operations. We will now define some others:
Rings
A set with addition and multiplication is a #~{ring} if it satisfies A1, A2, A3, A4, M1, D1 and D2. I.e. a ring obeys all the additive rules, is associative with respect to multiplication, and both right and left distributive.
A ring which also satisfies M3 and M4 (multiplicative identity and inverse) is called a #~{division ring}.
As can be seen, a field is a division ring which is multiplicatively commutative.
The real numbers, &reals., the rational numbers, Q, and the complex numbers, C, with the ususal operations of addition and multiplication, are all fields. The set of all integers is a ring (in fact it is a commutative ring with multiplicative identity, but it does not have multiplicative inverse).
The set of all ~n # ~n matrices over a particular field, is a ring under the usual operations of matrix addition and matrix multiplication.
Groups
A set S with one binary operation (denoted &comp. ) is a #~{group} if it satisfies G1 - G3 :
_ Associative Law: _ _ &forall. ~a, ~b, ~c &in. S:
G1. _ _ ( ~a &comp. ~b) &comp. ~c _ = _ ~a &comp. ( ~b &comp. ~c )
_ Identity Law: _ _ &forall. ~a &in. S:
G2. _ _ &exist. ~e &in. S _ such that _ ~a &comp. ~e _ = _ ~e &comp. ~a _ = _ ~a
_ Inverse Law:
G3. _ _ &forall. ~a &in. S, _ &exist. ~a#~' in S _ such that _ ~a &comp. ~a#~' _ = _ ~a#~' &comp. ~a _ = _ ~e
S is called an #~{Abelian group} if S is a group and satisfies:
_ Commutative Law: _ _ &forall. ~a, ~b &in. S:
_ _ ~a &comp. ~b _ = _ ~b &comp. ~a
A set with binary operation which is associative (G1 only) is called a #~{semigroup}.
A ring is an Abelian group under addition. The non-zero elements of a division ring form a group under multiplication. The non-zero elements of a field form an Abelian group under multiplication.
The set of all from a set S to itself is a group under the operation of , with identity &iota._S, and inverse defined by the .
Symmetries
If X &subseteq. &reals.^~n, a #~{symmetry} of X is a distance preserving bijective mapping _ &theta. #: X -> X _ (i.e. rotations, translations, reflections etc., and combinations thereof). So &forall. ~x, ~y &in. X , _ d ( ~x&theta. , ~y&theta. ) _ = _ d ( ~x , ~y ).
The symmetries of X form a group under composition, since if _ &theta. and &phi. are distance preserving bijective mappings, so are &theta.&phi., &theta.^{-1}
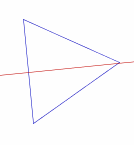 Consider the equilateral triangle shown right.
Consider the equilateral triangle shown right.
Then let &alpha. be the symmetry obtained by rotating the triangle through 2&pi.{/}3 radians (120° anticlockwise),
let &gamma. be the symmetry obtained by reflecting the triangle in the line shown.
If we now label the apexes of the triangle we can see that there are six symmetries of the triangle, which are shown below (as a result of applying each symmetry to the original (top-left) triangle), together with the combination of &alpha. and &gamma. - or &iota., the identity map - needed to obtain them:
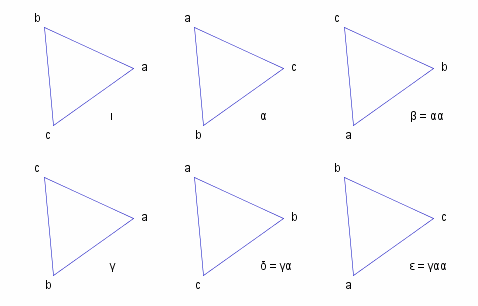
Note that there are more than one way to obtain a symmetry, for example the mapping _ &delta. = &gamma.&alpha. , _ could also be expressed _ &delta. = &alpha.^2&gamma.
Note also that _ &alpha.^2 = &alpha.^{-1} , _ so we have _ &gamma.&alpha. = &alpha.^{-1}&gamma..
We give each symmetry its own name, viz.
&iota. , _ &alpha. , _ &beta. ( = &alpha.^2 ) , _ &gamma. , _ &delta. ( = &gamma.&alpha. ) , _ &epsilon. ( = &gamma.&alpha.^2 )
_
| _ | &iota. | &alpha. | &beta. | &gamma. | &delta. | &epsilon. |
| &iota. | &iota. | &alpha. | &beta. | &gamma. | &delta. | &epsilon. |
| &alpha. | &alpha. | &beta. | &iota. | &epsilon. | &gamma. | &delta. |
| &beta. | &beta. | &iota. | &alpha. | &delta. | &epsilon. | &gamma. |
| &gamma. | &gamma. | &delta. | &epsilon. | &iota. | &alpha. | &beta. |
| &delta. | &delta. | &epsilon. | &gamma. | &beta. | &iota. | &alpha. |
| &epsilon. | &epsilon. | &gamma. | &delta. | &alpha. | &beta. | &iota. |
In the same way that &alpha. is a 1/3 rotation anti-clockwise, and &gamma. is a reflection (i.e. a ~{flip-over}) about the axis through the right hand apex, so &beta. is a 1/3 rotation clockwise, &delta. is a reflection about the axis through the bottom-left apex, and &epsilon. is a reflection about the axis through the top-left apex.
We can draw up the multiplication table (right):
Rotation
If X &subseteq. &reals.^3, a symmetry is called a #~{rotation} if it can be ~{realized by a rigid movement of the set X in &reals.^3}.
so the symmetry 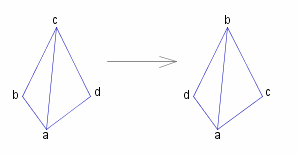 is a rotation,
is a rotation,
while 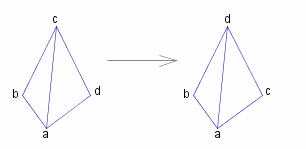 is not.
is not.
The set of all rotations of a set X &subseteq. &reals.^3 is a group under the operation of composition of mappings.
Source for the graphs shown on this page can be viewed by going to the .