Functions of a Random Variable
Adding Constant to Random Variables
~X is a random variable and _ ~Z = ~X + ~c , _ ~c &in. &reals. .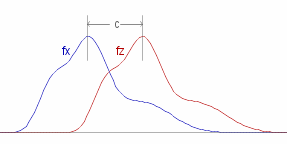
F_~Z ( ~z ) _ = _ P ( ~X + ~c < ~z ) _ = _ F_~X ( ~z - ~c )
f_~Z ( ~z ) _ = _ F#~'_~Z ( ~z ) _ = _ F#~'_~X ( ~z - ~c ) _ = _ f_~X ( ~z - ~c )
So the density and distribution functions are simply translated ~c units to the right (~c > 0) or left (~c < 0). (See diagram right.)
Scalar Product of Random Variables
~X is a random variable and _ ~Z = &alpha. ~X , _ &alpha. &in. &reals. .
F_~Z ( ~z ) _ = _ P ( &alpha.~X < ~z )
- Case 1) _ &alpha. > 0
-
F_~Z ( ~z ) _ = _ P ( ~X < ~z ./ &alpha. ) _ = _ F_~X ( ~z ./ &alpha. )
f_~Z ( ~z ) _ = _ fract{d F_~X ( ~z ./ &alpha. ), d~z} _ = _ fract{1, &alpha.} F#'_~X ( ~z ./ &alpha. ) _ = _ fract{1, &alpha.} f_~X ( ~z ./ &alpha. )
- Case 2) _ &alpha. < 0
-
F_~Z ( ~z ) _ = _ P ( ~X > ~z ./ &alpha. ) _ = _ 1 - F_~X ( ~z ./ &alpha. )
f_~Z ( ~z ) _ = _ - fract{d F_~X ( ~z ./ &alpha. ), d~z} _ = _ - fract{1, &alpha.} F#'_~X ( ~z ./ &alpha. ) _ = _ - fract{1, &alpha.} f_~X ( ~z ./ &alpha. )
Expressing this generally we write: _ _ f_~Z ( ~z ) _ = _ fract{1, |&alpha.|} f_~X ( ~z ./ &alpha. )
Square of Random Variables
~X is a random variable and _ ~Z = ~X ^2. _ If ~z < 0, then
F_~Z ( ~z ) _ = _ P ( ~X ^2 < ~z ) _ = _ 0
If ~z > 0 then
F_~Z ( ~z ) _ = _ P ( ~X ^2 < ~z ) _ = _ P ( | ~X | < &sqrt.$~z ) _ = _ P ( - &sqrt.$~z < ~X < &sqrt.$~z )
_ _ _ _ _ = _ F_~X ( &sqrt.$~z ) _ - _ F_~X ( - &sqrt.$~z )
f_~Z (~z) _ = _ fract{1,2&sqrt.$~z} F#'_~X ( &sqrt.$~z ) _ - _ fract{- 1,2&sqrt.$~z}F#'_~X ( - &sqrt.$~z ) _ = _ fract{1,2&sqrt.$~z} rndb{f_~X ( &sqrt.$~z ) _ + _ f_~X ( - &sqrt.$~z )}
~{Example}
For the the density function is symmetric about zero, i.e.
f_~X ( - ~x) _ = _ f_~X ( ~x ) _ = _ fract{1,&sqrt.${2&pi.}} exp rndb{fract{- ~x^2,2 }}
so if _ ~X ~ N( 0 , 1 ) _ and _ ~Z = ~X ^2
f_~Z ( ~z ) _ = _ fract{1,&sqrt.${2&pi.~z}} exp rndb{fract{- ~z,2 }}
This is the density function for a distribution with one degree of freedom.
Variance of Standard Normal Distribution
We defined the of a continuous random variable, and saw that:
var( ~X ) _ = _ E( ~X ^2 ) - E( ~X )^2
For the we saw that E ( ~X ) = 0 , so _ _ var( ~X ) _ = _ E( ~X ^2 )
But, as shown above _ ~X ^2 ~ &chi. ( 1 ) , _ and the random variable with one degree of freedom is 1, i.e.
~X ~ N ( 0 , 1 ) , _ then _ _ var ( ~X ) = 1.