Examples of Series
Geometric Series
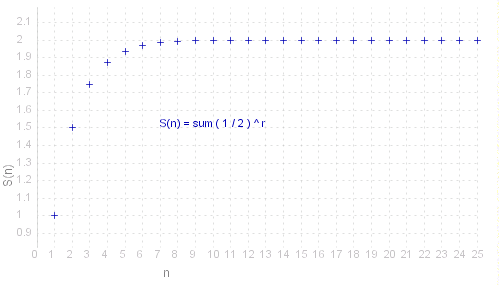
sum{~x^~k,~k = 0,&infty.} , _ _ _ _ e.g. _ _ 1 + 2 + 4 + 8 + 16 + ... , _ _ 1 + fract{1,2} + fract{1,4} + fract{1,8} + fract{1,16} + ...
We have
~x ~s_~n _ = _ ~x sum{~x^~k,~k = 0,~n } _ = _ sum{~x^~k,~k = 1,~n + 1} _ = _ ~s_{~n+1} - 1 _ = _ ~s_~n + ~x^{~n+1} - 1
so _ ( 1 - ~x ) ~s_~n = 1 - ~x^{~n+1} _ => _ ~s_~n = ( 1 - ~x^{~n+1} ) / ( 1 - ~x ).
~x^{~n+1} -> 0 _ as _ ~n -> &infty. _ providing | ~x | < 1, _ so _ ~s_~n -> 1 / ( 1 - ~x ) _ as _ ~n -> &infty. .
Exponential Series
~e _ = _ sum{fract{1,~k#!},~k = 0,&infty.} _ = _ 1 + fract{1,1#!} + fract{1,2#!} + fract{1,3#!} + ... + fract{1,~r#!} + f(~r)
where
f(~r) _ = _ sum{fract{1,~k#!},~k = ~r+1,&infty.} _ = _ fract{1,( ~r + 1 )#!} rndb{1 + fract{1,( ~r + 2 )} + fract{1,( ~r + 2 )( ~r + 3 )} ... }
_ _ < _ _ fract{1,( ~r + 1 )#!} sum{ script{rndb{fract{1,( ~r +1 )}},,, _ ~j,} ,~j = 0,&infty.} _ = _ fract{1,( ~r + 1 )#!} rndb{ fract{1,1 - 1/( ~r + 1 )}}
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ (geometric series)
_ = _ fract{1,( ~r + 1 )#!} fract{~r + 1,~r} _ = _ fract{1,~r#! ~r} _ _ -> _ _ 0 , _ as ~r -> &infty.
The number ~e is not rational, for suppose ~e = ~p / ~q, _ ~p, ~q &in. &naturals.. We have
~e _ = _ _ = _ 1 + 1 + fract{1,2#!} + fract{1,3#!} + ... + fract{1,~q#!} + f(~q)
~q#! fract{~p,~q} _ = _ ~q#! ~e _ = _ ~q#! + ~q#! + fract{~q#!,2#!} + fract{~q#!,3#!} + ... + 1 + ~q#! f(~q)
now ~q#! ( ~p / ~q ) _ = _ (~q - 1)#! ~p _ which is an integer, _ so ~q#! f(~q) must be and integer, as all the other terms are.
but _ 0 < f(~q) < 1 / (~q#! ~q) _ i.e. _ 0 < ~q#! f(~q) < 1/~q _ contradiction. 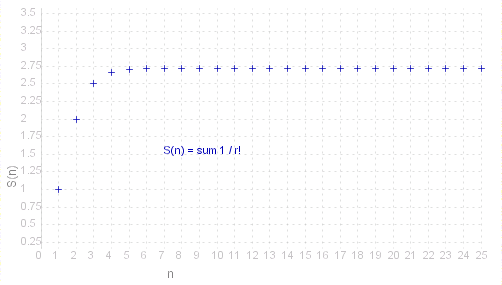
Harmonic Series
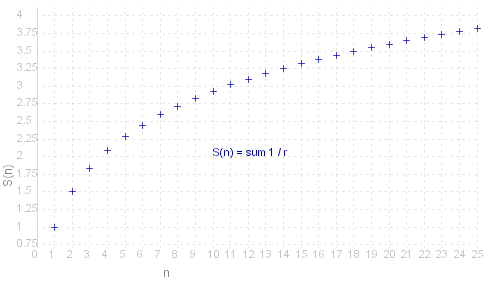
sum{fract{1,~n},~n = 1,&infty.} _ = _ 1 + fract{1,2} + fract{1,3} + fract{1,4} + fract{1,5} + fract{1,6} ...
Put
g(~r) _ = _ fract{1,2^~r + 1} + fract{1,2^~r + 2} + ... + fract{1,2^{~r+1}} , _ (2^~r terms)
_ _ > _ _ fract{1,2^{~r+1}} + fract{1,2^{~r+1}} + ... + fract{1,2^{~r+1}} _ = _ fract{2^~r,2^{~r+1}} _ = _ fract{1,2}
i.e. _ for ~r = 0 , _ g(~r) = fract{1,2} , _ _ for ~r = 1 , _ g(~r) = fract{1,3} + fract{1,4} = fract{7,12} > fract{1,2} , _ etc.
I.e. the series is unbounded and therefore divergent: _ _ &sum.(1/~n) _ -> _ &infty. .
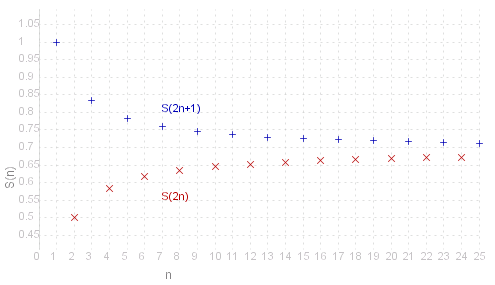
Alternating Harmonic Series
sum{fract{(-1)^{~n+1},~n},~n = 1,&infty.}
Source for the graphs shown here can be viewed by going to the diagram capture page .