Poisson Process
Poisson Process
A random or stochastic process where events occur in time is a #~{Poisson process} if it meets the following conditions:
- Events occur singly, ("#~{orderly}").
- The average rate of events is constant, ("#~{homogenous}").
- The occurence of events is independent of previous occurences, ("#~{memoryless}").
We will adopt the following notation:
- ~N ( ~s , ~t ) is the number of events in the interval [ ~s , ~t )
- ~T_1 is the time from the start of measurements to the first event.
- ~T_~n is the time between event ( ~n - 1 ) and event ~n , _ ( ~n > 1 ).
- ~W_~n - the waiting time - is the time from the start of measurements to the ~n^{th} event, _ ~W_~n = &sum._1^~n ~T_~n
Using some of the above notation, the conditions for a Poisson process can be expressed more formally:
|
where _ &omicron.( &delta.~t ) _ represents any function ( or really a category of functions) for which _ &omicron.( &delta.~t ) ./ &delta.~t -> 0 _ as _ &delta.~t -> 0 . _ Note that
- &omicron.( &delta.~t ) + &omicron.( &delta.~t ) _ = _ &omicron.( &delta.~t )
- ~c &omicron.( &delta.~t ) _ = _ &omicron.( &delta.~t ) , _ any ~c &in. &reals.
Note that a more precise formaulation of condition 1) would be
lim{{ P( ~N ( ~s , ~s + ~t + &delta.~t ) - ~N ( ~s , ~s + ~t ) > 1 | ~N ( ~s , ~s + ~t + &delta.~t ) - ~N ( ~s , ~s + ~t ) >= 1 ) },&delta.~t -> 0} _ = _ 0
Poisson Distribution
We wish to derive the distribution function for the number of events occurring in a time interval of length ~t. Choose arbitrarily any point in time ~s, define the functions p_~x ( ~t ):
- ~p_~x ( ~t ) _ #:= _ P ( ~N ( ~s , ~s + ~t ) = ~x ) _ = _ prob. of ~x events in the time interval [ ~s , ~s + ~t ) > 0
Note that _ ~p_~x ( ~t ) &downarrow. 0 _ as _ ~t &downarrow. 0 , _ ~x > 0 , _ while _ ~p_0 ( ~t ) &uparrow. 1 _ as _ ~t &downarrow. 0 . _ We therefore stipulate
- ~p_0 ( 0 ) _ #:= _ 1
- ~p_~x ( 0 ) _ #:= _ 0 , _ _ ~x > 0
To start consider the function p_0 ( ~t ). We will derive a differential equation in p_0 and solve it.
Now
~p_0 ( ~t + &delta.~t ) _ = _ P #( ~N ( ~s , ~s + ~t ) = 0 _ and _ ~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 0 #)
_ _ _ _ = _ P ( ~N ( ~s , ~s + ~t ) = 0 ) # P (~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 0 ) , _ _ _ ( by 3)
Substituting from 2. in 1. we get:
P (~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 0 ) _ = _ 1 - λ &delta.~t + &omicron.( &delta.~t )
so
~p_0 ( ~t + &delta.~t ) _ = _ ~p_0( ~t ) # ( 1 - λ &delta.~t + &omicron.( &delta.~t ) )
fract{~p_0 ( ~t + &delta.~t ) - ~p_0( ~t ),&delta.~t} _ = _ - λ ~p_0( ~t ) + fract{&omicron.( &delta.~t ),&delta.~t} ~p_0( ~t )
and taking the limit as &delta.~t -> 0
fract{d~p_0,d~t}( ~t ) _ = _ - λ ~p_0( ~t )
Solve this differential equation by separating variables , i.e.
int{,,,}fract{1,~p_0( ~t )}d~p_0 _ = _ - int{,,,}λ d~t _ _ => _ _ ln ( ~p_0( ~t ) ) _ = _ - λ ~t + ~c
using the "initial condition" that _ ~p_0( 0 ) = 1 , _ then for _ ~t = 0 _ we get
_ _ ~c _ = _ ln ( ~p_0( 0 ) ) + λ 0 _ = _ ln ( 1 ) + 0 _ = _ 0
so
| ~p_0( ~t ) _ = _ e^{- λ ~t} |
Now consider the functions _ ~p_~x , _ ~x &in. &naturals.. _ _ ~p_~x ( ~t + &delta.~t ) _ = _ P ( ~N ( ~s , ~s + ~t + &delta.~t ) = ~x ).
The event _ [ ~N ( ~s , ~s + ~t + &delta.~t ) = ~x ] _ can be considered as the union of three disjoint events:
[ ~N ( ~s , ~s + ~t + &delta.~t ) = ~x ) ] _ #{=} _ ( [ ~N ( ~s , ~t ) = ~x ] and [ ~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 0 ] )
_ _ _ _ _ _ _ _ _ _ _ &union. _ #( [ ~N ( ~s , ~t ) = ~x - 1 ] and [ ~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 1 ] #)
_ _ _ _ _ _ _ _ _ _ _ &union. _ #( [ ~N ( ~s , ~t ) < ~x - 1 ] and [ ~N ( ~s + ~t , ~s + ~t + &delta.~t ) > 1 ] #)
So
~p_~x ( ~t + &delta.~t ) _ = _ ~p_~x( ~t ) _ # _ P ( ~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 0 )
_ _ _ _ _ _ _ _ + _ ~p_{~x - 1}( ~t ) _ # _ P ( ~N ( ~s + ~t , ~s + ~t + &delta.~t ) = 1 )
_ _ _ _ _ _ _ _ + _ P[ ~N ( ~s , ~s + ~t ) < ~x - 1 ] _ # _ P[ ~N ( ~s + ~t , ~s + ~t + &delta.~t ) > 1 ]
_ _ _ = _ ~p_~x( ~t ) # ( 1 - λ &delta.~t + &omicron.( &delta.~t ) ) _ + _ ~p_{~x - 1}( ~t ) # ( λ &delta.~t + &omicron.( &delta.~t ) ) _ + _ P[ ~N ( ~s , ~t ) < ~x - 1 ] # &omicron.( &delta.~t )
_ _ _ = _ ~p_~x( ~t ) # ( 1 - λ &delta.~t ) _ + _ ~p_{~x - 1}( ~t ) # ( λ &delta.~t ) _ + _ &omicron.( &delta.~t )
[ remember that _ ~{anything} # &omicron.( &delta.~t ) _ = _ &omicron.( &delta.~t ) ]
re-arranging, and dividing by &delta.~t:
fract{~p_~x ( ~t + &delta.~t ) - ~p_~x( ~t ),&delta.~t} _ = _ λ ~p_{~x - 1}( ~t ) _ - _ λ ~p_~x( ~t ) _ + _ &omicron.( &delta.~t )
Taking limits we obtain the series of differential equations:
| ~p_~x#' ( ~t ) + λ ~p_{~x}( ~t ) _ = _ λ ~p_{~x - 1}( ~t ) , _ _ ~x &in. &naturals. |
We will show by induction that _ ~p_~x( ~t ) _ = _ fract{( λ~t ) ^~x ~e ^{- λ~t},~x #!}
This is true for ~x = 0, now suppose that it is true for (~x - 1), where ~x > 0, i.e.
~p_{~x - 1}( ~t ) _ = _ fract{( λ~t ) ^{~x - 1} ~e ^{- λ~t},(~x - 1) #!}
Multiplying the above differential equation by the integration factor ~e^{λ~t}:
~e^{λ~t}~p_~x#' ( ~t ) + λ ~e^{λ~t} ~p_{~x}( ~t ) _ = _ λ fract{( λ~t ) ^{~x - 1},(~x - 1) #!}
i.e.
fract{d,d~t} ~e^{λ~t} ~p_{~x}( ~t ) _ = _ fract{ λ^~x ~t ^{~x - 1},(~x - 1) #!}
~e^{λ~t} ~p_{~x}( ~t ) _ = _ fract{ λ^~x ~t ^~x ,~x (~x - 1) #!} _ + _ ~c _ = _ fract{ ( λ~t ) ^~x ,~x #!} _ + _ ~c
Applying the initial condition ~p_~x ( 0 ) = 0 _ => _ ~c = 0, which completes the proof.
So we can conclude that if ~N ( ~t ) is the number of events in any interval of length ~t in a Poisson process then
|
P ( ~N ( ~t ) = ~x ) _ = _ fract{( λ~t ) ^~x ~e ^{- λ~t},~x #!} , _ _ ~x = 0, 1, ... |
Waiting Times
~W_~n is the time from the ~n-1^{th} event to the the ~n^{th} event . (The 0^{th} event being the observation start time.)
P ( ~W_~n > ~t ) _ = _ P ( no events in [ ~s, ~s + ~t ) ) , _ where the ~n-1^{th} event is at time ~s.
_ _ _ _ _ _ _ = _ P ( ~N(~t) = 0 ) _ = _ e ^{-&lambda.~t}
F_{~W_~n} ( ~t ) _ #:= _ P ( ~T_1 =< ~t ) _ = _ 1 - e ^{-&lambda.~t}
Inter Event Time
~T_1 is the time to the first event. ~T_1 = ~W_1 so :
P ( ~T_1 > ~t ) _ = _ e ^{-&lambda.~t}
~T_2 is the time to the second event:
P ( ~T_2 > ~t ) _ = _ P ( no events in [0, ~t) ) + P ( one event in [0, ~t) )
_ _ _ _ _ _ _ = _ e ^{-&lambda.~t} _ + _ λ~t ~e ^{- λ~t}
But _ ~T_2 = ~W_1 + ~W_2 , _ and these are independent, so
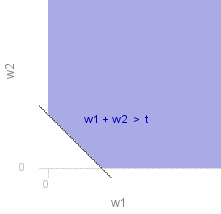
P ( ~T_2 > ~t ) _ = _ P ( ~W_1 + ~W_2 > ~t ) _ = _ &integ.&integ._~A f (~w_1)f (~w_2) d~w_2 d~w_1
where ~A is the area shown shaded in the graph on the right.
_ _ _ _ _ _ _ = _ dblint{&lambda.^2 ~e^{-&lambda.(~w_1 + ~w_2)},0,~t,~t - ~w_1,&infty.,d~w_2 d~w_1} _ + _ dblint{&lambda.^2 ~e^{-&lambda.(~w_1 + ~w_2)},~t,&infty.,0,&infty.,d~w_2 d~w_1}
_ _ _ _ _ _ _ = _ int{script{sqrb{ -&lambda. ~e^{-&lambda.(~w_1 + ~w_2)}},,,&infty.,~t - ~w_1},0,~t,d~w_1} _ + _ int{script{sqrb{ -&lambda. ~e^{-&lambda.(~w_1 + ~w_2)}},,,&infty.,0},~t,&infty.,d~w_1}
_ _ _ _ _ _ _ = _ int{&lambda. ~e^{-&lambda.~t},0,~t,d~w_1} _ + _ int{&lambda. ~e^{-&lambda.~w_1},~t,&infty.,d~w_1}
_ _ _ _ _ _ _ = _ script{sqrb{ &lambda. ~w_1 ~e^{-&lambda.~t}},,,~t,0} _ + _ script{sqrb{ - ~e^{-&lambda.~w_1}},,,&infty.,~t} _ = _ λ~t ~e ^{- λ~t} _ + _ e ^{-&lambda.~t}
Confirming our earlier finding.
Source for the graphs shown on this page can be viewed by going to the diagram capture page .