Conics Definition
Conic Equation
A conic section is the locus of points where the proportion of the distance from any of the points to a fixed point, called the #~{focus} and the perpendicular distance from the same point to a straight line, called the #~{directrix}, is a fixed number ~e, called the #~{excentricity}.
Suppose we set the #~{focus} at the point ( ~a , 0 ), where the section passes through the point ( 0 , 0 ), so the directrix is the straight line parallel to the y-axis at _ ~a ./ ~e _ from the axis.
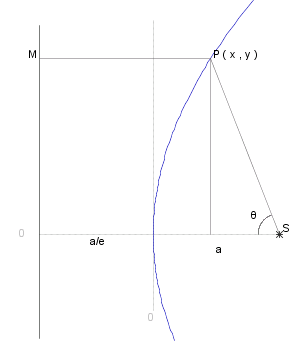
In the diagram (right) we have _ _ SP _ = _ ~e PM . _ _ So
( ~a - ~x )^2 + ~y^2 _ = _ SP^2 _ = _ ~e^2 PM^2
_ _ _ _ _ _ = _ ~e^2 ( ~a ./ ~e _ + _ ~x )^2 _ = _ ( ~a + ~e ~x )^2
~y^2 _ = _ ~a^2 + ~e^2~x^2 + 2 ~a ~e ~x - ~a^2 - ~x^2 + 2 ~a ~x
|
_ _ ~y^2 _ = _ ( ~e^2 - 1 ) ~x^2 + 2 ~a ( ~e + 1 ) ~x |
Parametric Equation
We can also describe the curve in terms of the angle &theta. as shown on the diagram
( ~a - ~x ) _ = _ PS cos &theta. _ = _ ~e PM cos &theta. _ = _ ( ~a + ~e~x ) cos &theta.
|
~x _ = _ fract{~a ( 1 - cos &theta. ), 1 + ~e cos &theta.} |
~y _ = _ PS sin &theta. _ = _ ( ~a + ~e~x ) sin &theta.
_ _ _ _ = _ fract{( ~a + ~a~e cos &theta. ) + ~a~e ( 1 - cos &theta. ), 1 + ~e cos &theta.} sin &theta.
|
~y _ = _ fract{~a ( 1 + ~e ) sin &theta., 1 + ~e cos &theta.} |
Conic Types
So far the only restrictions we have placed on the parameters, albeit implicitly, is that ~a is positive, and ~e is non-negative.
~y^2 _ = _ ( ~e^2 - 1 ) ~x^2 + 2 ~a ( ~e + 1 ) ~x , _ _ ~a > 0 , _ ~e >= 0 ,
consider the expression
~z _ = _ ( ~e^2 - 1 ) ~x^2 + 2 ~a ( ~e + 1 ) ~x
which we can write
~z _ = _ ~p ~x^2 + ~q ~x _ = _ ~x ( ~p ~x + ~q )
where _ _ ~p = ( ~e^2 - 1 ), _ ~q = 2 ~a ( ~e + 1 ), _ so _ -1 =< ~p < &infty. ,_ and _ 0 =< ~q < &infty.
Now ~y has real roots only if ~z is non-negative, which is the case if:
~x >= 0 _ and _ ( ~p ~x + ~q ) >= 0 <=> \{ ~x >= - ~q ./ ~p , ~p positive | ~x =< - ~q ./ ~p , ~p negative \} _ _ (1)
~x =< 0 _ and _ ( ~p ~x + ~q ) =< 0 <=> \{ ~x =< - ~q ./ ~p , ~p positive | ~x >= - ~q ./ ~p , ~p negative \} _ _ (2)
[Note that ~q is always positive, and ~p is positive if ~e > 1.]
So, if ~p > 0, ~y has real roots if
~x > 0 _ (1) _ _ or _ _ ~x < - ~q ./ ~p _ (2)
If ~p < 0, ~y has real roots if
0 < ~x < - ~q ./ ~p _ (1) _ _ or _ _ - ~q ./ ~p < ~x < 0 _ (2) - contradiction as - ~q ./ ~p > 0
If ~p = 0 then ( ~p ~x + ~q ) = ~q which is always positive, so ~y has positive roots only if ~x >0.
Hyperbola
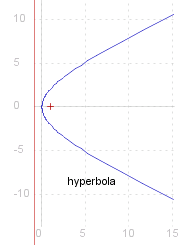
~p is greater than zero when #{~e is greater than 1}. In this case, as shown above, ~y has real roots in the region
_ _ ~x _ < _ -~q ./ ~p _ = _ - 2 ~a ( ~e + 1 ) ./ ( ~e^2 - 1 ) _ = _ - 2 ~a ./ ( ~e - 1 )
and the region
_ _ ~x _ > _ 0
When ~e is greater than 1 the curve is known as a #~{hyperbola}
Parabola
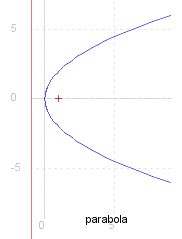
~p is equal to zero when #{~e is equal to 1}. In this case ~y has real roots in the region
_ _ ~x _ > _ 0
When ~e is equal to 1 the curve is known as a #~{parabola}
Elipse
~p is less than zero when #{~e is less than 1}. In this case ~y has real roots in the region
_ _ 0 _ < _ ~x _ < _ -~q ./ ~p _ = _ 2 ~a ./ ( 1 - ~e )
When ~e is less than 1 the curve is known as an #~{elipse}
Source for the graphs shown here can be viewed by going to the diagram capture page .