Trigonometry

Consider a right angled triangle (drawn in red) with hypotenuse ~a, and shorter sides ~b and ~c as shown.

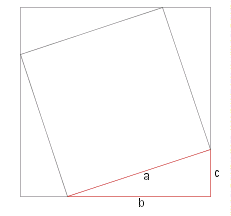
Draw three other "copies" of the triangle as shown. Now:

Area of red triangle = ~b~c / 2

Area of large square = (~b + ~c)^2 = ~b^2 + ~c^2 + 2~b~c

Area of small square = ~a^2

But the large square is just the sum of the small square and the four triangles. _ So:

~b^2 + ~c^2 + 2~b~c = ~a^2 + 2~b~c

So _ _ _ ~b^2 + ~c^2 = ~a^2

Trigonometrical Definitions

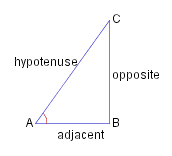
With reference to the right-angled triangle (right): _ _ _ sine A _ ( #:=#: _ sin A ) _ #:= _ opposite ./ hypotenuse . cosine A _ ( #:=#: _ cos A ) _ #:= _ adjacent ./ hypotenuse . tangent A _ ( #:=#: _ tan A ) _ #:= _ opposite ./ adjacent .

#{Mnemonic}
~some ~officers ~have _ ~curly ~auburn ~hair _ ~to ~offer ~attraction.
~sine = ~opposite ./ ~hypotenuse , _ ~cosine = ~adjacent ./ ~hypotenuse , _ ~tangent = ~opposite ./ ~adjacent .

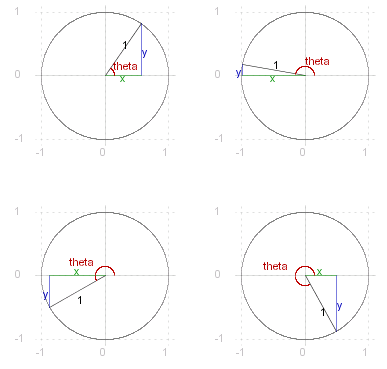
To define sine and cosine of the general angle, consider a circle of unit radius drawn with centre at the origin. Four Examples are shown below, with the angle &theta. in each quadrant. From our elementary definitions, and considering the first diagram, we can put :

 

_ _ _ sin &theta. _ #:= _ ~y ./ 1 _ = _ ~y
_ _ _ cos &theta. _ #:= _ ~x ./ 1 _ = _ ~x
_ _ _ tan &theta. _ #:= _ ~y ./ ~x _ = _ sin &theta. ./ cos &theta.

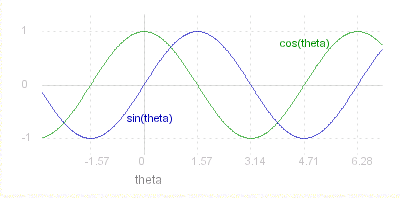
Here is a plot of _ sin &theta. _ and _ cos &theta. _ against _ &theta. _ (in radians):

Finally we define the other trigonometrical quantities :

 

_ _ _ cosecant &theta. _ [ #:=#: _ cosec &theta. ] _ #:=#: _ 1 ./ sin &theta.
_ _ _ secant &theta. _ [ #:=#: _ sec &theta. ] _ #:= _ 1 ./ cos &theta.
_ _ _ cotangent &theta. _ [ #:=#: _ cotan &theta. ] _ #:= _ 1 ./ tan &theta.

Compound Angles

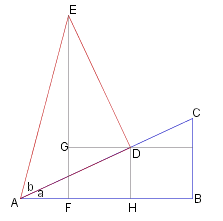
Consider the right-anlgled triangles &triangle.ABC and &triangle.ADE [The right-angles being at B and D respectively], where AC = AE = 1, and &angle.BAC = ~a, and &angle.DAE = ~b.

Drop the vertical from E to meet AB at F, and draw the horizontal through D to meet the vertical at G. Drop the vertical from D to meet AB at H. Note that &angle.GED = ~a. We have:

ED = sin(~b) _ so EG = cos(~a) sin(~b)

AD = cos(~b) _ so DH = sin(~a)cos(~b)

EF = EG + GF = EG + DH _ = cos(~a) sin(~b) + sin(~a)cos(~b)

but _ EF = sin(~a + ~b), so

sin(~a + ~b) = cos(~a) sin(~b) + sin(~a)cos(~b)

similarly:
cos(~a + ~b) = AF = AH &minus. FH = AH &minus. GD = cos(~a)cos(~b) &minus. sin(~a)sin(~b)

sin(~a + ~b) _ = _ cos(~a) sin(~b) + sin(~a)cos(~b) cos(~a + ~b) _ = _ cos(~a)cos(~b) &minus. sin(~a)sin(~b)

when ~a = ~b:

sin(2~a) _ = _ 2 cos(~a) sin(~a) cos(2~a) _ = _ cos^2(~a) &minus. sin^2(~a)

Area of Triangle

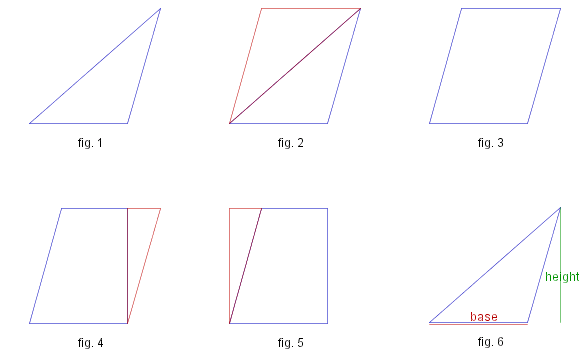
By studying the diagrams on the right you should be able to convince yourself that the area of any triangle is half the length of it's base (i.e. any side you wish to choose) times it's height (i.e. the length of the perpendicular from the base to the opposite apex. (See fig. 6). For any triangle (fig. 1) take two copies (fig. 2) to make a rhombus or parallelogram (fig. 3). Move the red triangle shown (fig. 4) over to the left to give the rectangle (fig. 5) whose area is base times height, and is just twice the area of the original triangle.

Sine Rule

~c : sin ~C _ = _ ~a : sin ~A _ = _ ~b : sin ~B

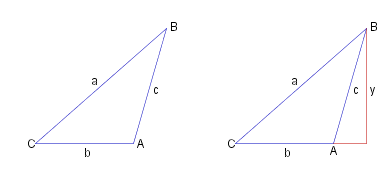~{area} &triangle. = &hlf. # ~{height} # ~{base} = &hlf. # ~y # ~b . First consider the acute &angle. ~C sin ~C = ~y / ~a _ => _ ~y = ~a sin ~C _ => _ ~{area} = &hlf. # ~a~b sin ~C &angle. ~B is also acute so by symmetry _ ~{area} = &hlf. # ~a~c sin ~B . &angle. ~A obtuse _ sin ~A = sin ( &pi. - ~A ) = ~y / ~c _ => _ ~y = ~c sin ~A _ => _ ~{area} = &hlf. # ~b~c sin ~A ~a~b sin ~C _ = _ ~b~c sin ~A _ = _ ~c~a sin ~B

Cosine Rule

~a^2 = ~c^2 + ~b^2 - 2~b~c cos ~A

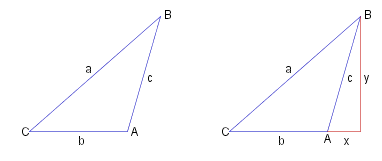
~a^2 = ~y^2 + (~b + ~x)^2 _ = ~y^2 + ~b^2 + ~x^2 + 2~b~x _ = (~c^2 - ~x^2) + ~b^2 + ~x^2 + 2~b~x _ = ~c^2 + ~b^2 + 2~b~x but _ ~x = ~c cos ( &pi. - ~A ) = - ~c cos ~A ~a^2 = ~c^2 + ~b^2 - 2~b~c cos ~A

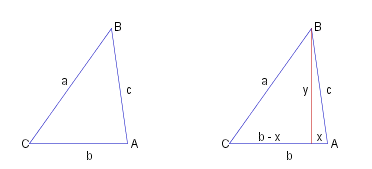~a^2 = ~y^2 + (~b - ~x)^2 _ = ~y^2 + ~b^2 + ~x^2 - 2~b~x _ = (~c^2 - ~x^2) + ~b^2 + ~x^2 - 2~b~x _ = ~c^2 + ~b^2 - 2~b~x but _ ~x = ~c cos ~A ~a^2 = ~c^2 + ~b^2 - 2~b~c cos ~A

---